超硬材料网

　　1 引言
　　
　　刀具磨损的检测方法通常可分为直接测量法和间接测量法两类。直接测量法就是直接测量刀具后刀面磨损带中间部分的平均磨损量；而间接测量法则是通过测量与刀具磨损有关的物理量(如切削力、声发射等)，并根据它们与刀具磨损之间的对应关系来判别刀具磨损情况。
　　
　　常用的一种间接测量法是选取切削分力的比值和该比值的变化作为判别刀具磨损的特征量，一旦这两个特征量超过某一阈值，即判定刀具已经磨损。但在应用该方法对刀具磨损进行实际检测时，由于振动和随机噪声的干扰，很容易出现误判。此外，由于刀具的正常磨损与异常磨损之间的界限具有不确定性，因此对判别阈值的预先设定比较困难，必须依靠经验和多次切削试验才能确定。另外该方法在不同的应用场合性能不够稳定。为此，本文提出一种新的间接测量方法，即利用小波变换对切削力信号进行分析，通过计算切削力信号的奇异性指数来实现对刀具磨损的检测。2 奇异性指数与刀具磨损的对应关系
　　
　　若信号f(t)在某点出现突变或某阶导数不连续，则称信号在该点具有奇异性，一般用Lipschitz 指数(简称Lip指数)来描述信号f(t)的奇异性程度。设有非负整数n，n≤a≤n+1，如果存在常数A>0以及n 次多项式pn(t)，对于t∈(t0-d，t0+d)时下式成立：
　　|f(t)-pn(t-t0)|≤A|t-t0|a
　　
　　(1)
　　
　　则称f(t)在t0处是Lipa的。如果f(t)在t0的Lip指数a<1，则称t0为f(t)的奇异点。
　　
　　Lip指数给出了信号f(t)在t0点可导性的精确信息。若n≥1，则f(t)在t0处n阶可导，第n阶导数在t0点具有奇异性，且pn(t-t0)为f(t)在t0处的Taylor 级数的前n+1 项；当n=0 时，pn(t-t0)=f(t0)，则由(1)式可知阶跃信号在阶跃点处a=0。若信号f(t)无限次可导，则该信号不具有奇异性。
　　
　　在切削加工中，当刀具磨损时，切削力会随之增大，且切削力在不同磨损阶段的差异可反映刀具的实际磨损状态。如果切削力信号突然上升或下降，则预示着刀具可能折断。由此可见，当刀具磨损时，相应的切削力信号存在奇异性，且奇异性指数的大小与刀具磨损状态具有一定对应关系，即刀具的磨损状态决定着切削力信号变化的剧烈程度，而奇异性指数正是用于描述这种剧烈程度的一个指标。刀具磨损越严重，相应的切削力信号变化越剧烈，Lip指数也越小；当刀具折断时，切削力信号会发生突变，此时对应的Lip指数a=0；Lip指数越接近于1，则说明切削力越平稳，刀具的磨损程度也越轻。由此可知，通过Lip指数对切削力信号变化程度的描述，可以真实反映刀具磨损状态。基于上述分析，本文将刀具磨损分为5种状态，每一种状态对应于某一范围的切削力信号Lip指数(见表1)，这样就在刀具磨损与Lip指数a之间建立了直接联系，实际检测时通过计算切削力信号的Lip指数，根据表1即可确定刀具的磨损状况。

　　3 信号奇异性的小波检测原理
　　
　　小波变换是检测信号奇异性的有效工具。小波Ø(t)在L2(R)中满足容许性条件∫RØ(t)dt=0，小波变换可定义为信号f与小波伸缩系的卷积，即
　　

Wf(s，x)=fØs(x)=	1	∫		f(t)Ø	(x-t)	dt
	s		R		s

　　式中，s为小波的尺度参数。
　　
　　对于小波的奇异性检测效果，有些文献给出了如下定理：若f(t)在t0点的Lip指数为a，且0　　

|Wf(s，x)|≤Asa

(3)

　　当尺度s→0 时，Wf(s，x)在t0点趋于零的速度为sa，小于Wf(s，x)在其它点趋于零的速度s，因此，当尺度s较小时，f(t)的小波变换在t0点取得极大值。
　　
　　对于两个尺度si，si+1，由式(3)两端取对数并相减，可得
　　

a=tan	|	Wf(si+1，x)	|	/lg(	si+1	)
		Wf(si，x)			si

　　式(4)表明，以lgs为横坐标、lg|Wf|为纵坐标的模极大值曲线上相邻两点的斜率就是信号在奇异点处的Lip 指数。

　4 试验与分析

　　在CM6140 车床上进行刀具磨损检测试验。试验条件为：工件材料：45 钢(调质)；刀具：YT15 硬质合金刀片(g0=25°，a0=5°，Kr=45°，ls=0°)；切削用量：vc=1.65m/ s，ap=3mm，f=0.2mm/r；测力仪：瑞士KISTLER公司9257A1型压电晶体测力仪，采用5006 型电荷放大器，采样频率为100Hz。
　　
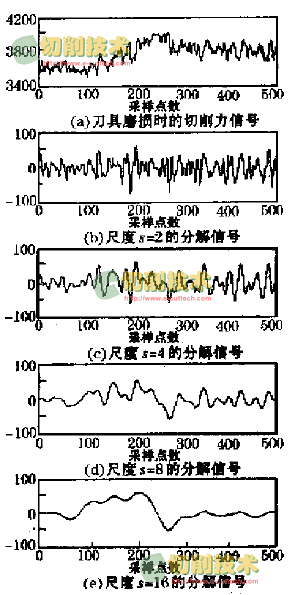
　　图1a所示为试验测得的刀具磨损时的一个切削力信号，由于背景噪声较大，因此切削力的变化曲线较平滑。采用小波变换则可将切削力的变化从背景噪声中检测出来。设N(x)是一个方差为s2 的白噪声，它实际上是一种Lip指数为-0.5-e(e>0)的随机分布，其小波变换的平均功率为E|Wf(s，x)|2=s2‖y‖/ s，它随着尺度的增大而迅速减小，这也是小波变换的另一优点。
　　
　　以Gauss小波为小波基，对图1a所示切削力信号在4个尺度上进行变换，得到各尺度上的信号分别如图1b、c、d、e所示。可以看出，当尺度较小时，模极大值的数目急剧增加，此时的模极大值主要由测量过程中的噪声所支配，因此难以据此分析切削力的真实变化情况。但随着尺度的增大，模极大值的数目迅速减少。当尺度s=16时(如图1e所示)，噪声所产生的模极大值已基本消失，仅在采样点n=61，116，147，196，251，320，389，448处还存在模极大值，且这些采样点处的模极大值在各个尺度上均存在，因此可以确定这是由信号本身的奇异性所产生的。由图1e可见，切削力在n=61处已开始波动，然后在n=116，147处进一步加强，最终在n=196处发生剧烈变化；随后又在n=251处骤然下降，在n=320，389，448等处反复波动，这种变化反映了刀具的磨损过程。根据这些点在各尺度上的小波变换值，利用式(4)可计算出它们的Lip指数(见表2)。

　　根据表1所示Lip指数与刀具磨损状态的对应关系，由表2所示Lip指数可判断出刀具的磨损有一个积累过程，并可判定刀具发生了较严重的磨损。对该刀具后刀面磨损带的直接测量结果(磨损量为0.382mm)证明本试验的分析结果与实际情况相符，正是这种磨损导致了切削力的波动。5 结论
　　
　　刀具磨损时的切削力信号存在奇异性，奇异性的大小与刀具磨损的剧烈程度有关。利用小波变换可检测出这种奇异性，并能计算出奇异性指数的大小，从而可实现对刀具磨损状态的正确判定。