超硬材料网

       摘要：复合加工工艺（HMP’s）相对于传统加工工艺，能够加工难切割材料并具有竞争力的价格优势。本文通过对铬镍铁合金718进行放电金刚石表面磨削加工（EDDSG）来进行建模，并研究其材料去除率（MRR）；MRR是低成本高效益的一个加工参数。在进行EDDSG前后用扫描电子显微镜（SEM）进行观察并验证了该工艺的实际效益。利用响应曲面法（RSM）中的旋转中心组合设计（CCRD）对实验进行规划和分析。建立了EDDSG输入参数（砂轮速度、脉冲电流、占空因数）间的数学关系。利用人工神经网络算法（ANN）对RSM进行建模。MRR预测值和实验结果匹配。
       关键词：EDDSG，铬镍铁合金718，响应曲面法，SEM
1. 引言
       镍基合金是应用最为广泛的超合金，占整个航天发动机制备材料的50%，特别是在燃气涡轮机室制造方面；在高温环境下耐腐蚀、耐机械疲劳、耐热疲劳、抗蠕变和耐磨损性能好。而加工这些机械性能优越的难切割材料也是非传统加工工艺的一个棘手问题。复合加工工艺（HMP’s）则是解决该问题的其中一个方案。
       HMP’s 集成了众多单一加工工艺的优势，又将单一工艺的劣势降到最低。HMP’s基于多个可控制的加工工艺机理同时对工艺性能产生影响从而提高加工精度。放电加工（EDM）是一种常见的加工工艺，放电脉冲能量对工件的表面整体性能有一定影响，导致微裂缝、降低材料的抗疲劳强度等。为解决EDM工艺中这一问题，Koshyet等人将金刚石磨削和EDM结合起来，即放电金刚石磨削技术（EDDG）来加工导电材料。Sanjeev Kumar 指出，在电火花作用下，通过热软化工件材料，磨削力得到了大大的降低。
       Yadavet将EDDG装置分为三个不同的构造部分，如图一所示：放电金刚石切断磨削（EDDCG）、放电金刚石平面磨削（EDDFG）和放电金刚石表面磨削（EDDSG）。EDDCG是利用砂轮的周边面，通过研磨和打火花将工件切割成条或者在工件上加工沟槽。EDDFG是利用砂轮的抛光面，通过研磨和打火花对工件端面进行加工；EDDSG是利用砂轮周边面，通过研磨和打火花对工件平面进行加工。

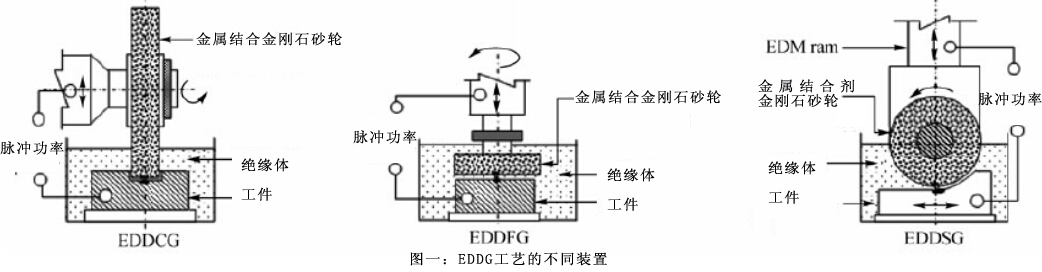
       根据以上文献综述，鲜有研究利用EDDSG工艺对新型先进材料如铬镍铁合金718进行加工。因此，本论文旨在研究铬镍铁合金718的EDDSG加工工艺。利用RSM和ANN技术求得的MRR预测值和实验结果相匹配。
2. 实验
       所有实验都在ENC 35 EDM上进行；图二为EDDSG装置，由青铜结合剂金刚石砂轮、直流电机、柄轴、V型带、轴承和交流可逆同步电动机组成，如图三所示。通过特殊装置将青铜结合剂金刚石砂轮固定在机器上，ZNC EDM机的伺服系统用来保持两个电极的间隔。表二为金刚石砂轮的规格。



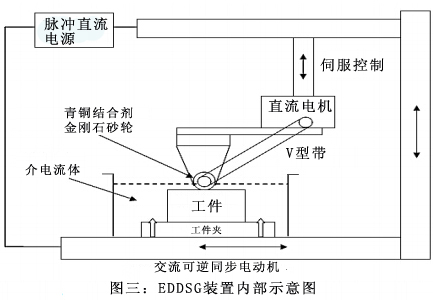
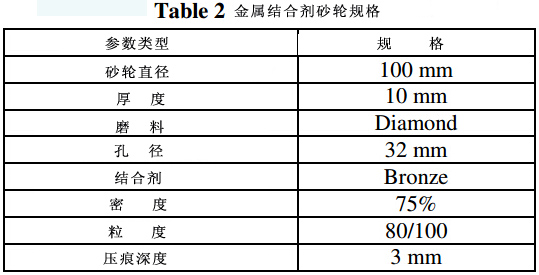
       砂轮和工件之间的间隙取决于间隙电压装置的绝缘击穿强度。柄轴用于自旋转和带动砂轮旋转，因此柄轴的设计就需要一些输入参数，如材料、直径、RPM、电机功率等。柄轴直径19mm，材料为EN24，轴承标准为ISI No. 1203。驱动砂轮旋转的电机为2HP、46000rpm的永磁直流电机（PMDC）。V型传送带为13mm×9mm，传送带的梯形截面有利于和滑轮保持接触以防止滑落。PMDC速度是可控的；通过自动进给装置实现工作台的往复运动，以此来保持砂轮和工件的相对运动。所有实验都按照平面磨削模式操作。铬镍铁合金718为本实验的材料，其组份如表3所示。


       砂轮速度、脉冲电流、脉冲间隔和占空因数为控制系数，MRR为性能参数。每一个输入参数值都有中间试验求得。表4为控制系数的实际值。根据CCRD对每个因子最少3个准级的要求进行实验。本实验中，选用标准的CCRD矩阵，四个控制系数三个准级七个中心点；共计31组实验。表5为实验结果和编码变量。



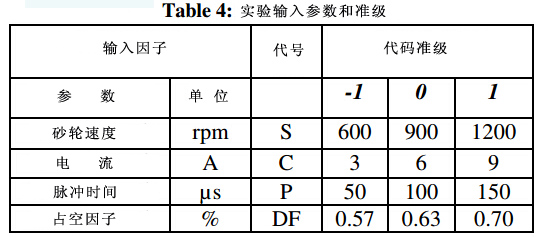
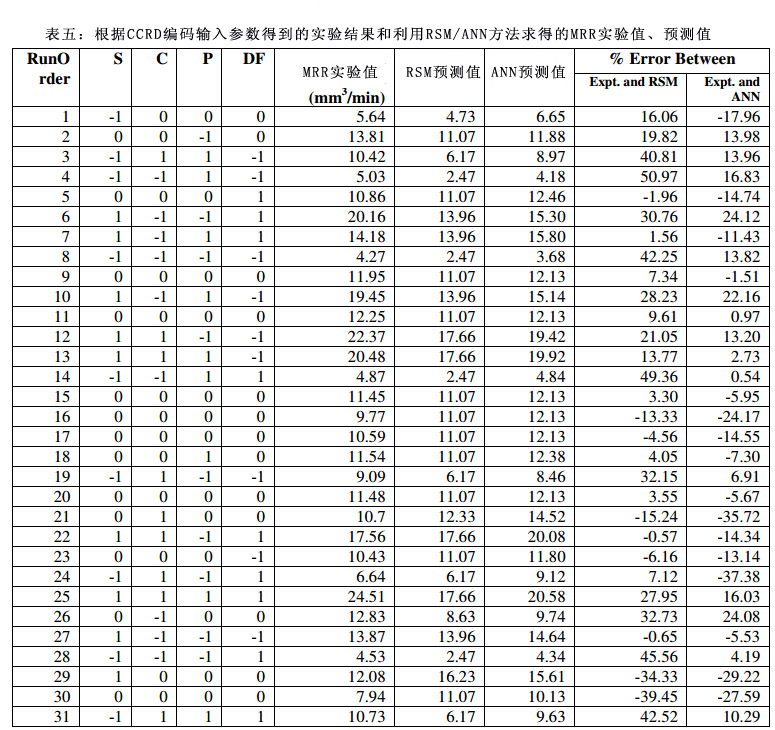
       所有实验都在60mm×10mm的铬镍铁合金718材料上进行操作，30分钟。用高精度电子天平对加工前后的材料进行称量。砂轮速度由数字转速计测得。
3. 数学模型
3.1 响应曲面法（RSM）
       RSM是将数学和统计相结合的一种研究方法，用于分析若干独立变量对一个非独立变量的影响，其目标是优化响应值。在诸多实验条件下，可以以定量形式表示独立因子，如公式（1）所示。


       在响应值Y和定量因子中，函数φ叫做相应曲面，或响应函数。
       相应曲面Y的一阶多项式如公式（2）所示：


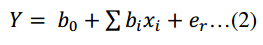
       公式3为MRR表达式：


3.2 模型适宜度检测
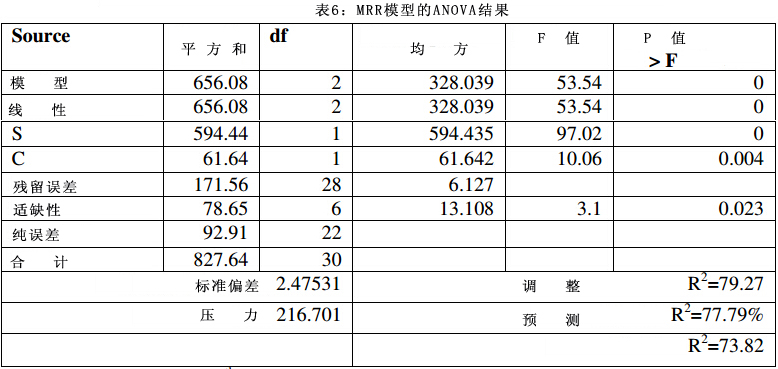
       实验用变量分析技术（ANOVA）对模型的适宜度进行检测，表6为二阶响应面结果。决定系数（R2）表示模型的适宜程度。决定系数值（R2=0.96998）表明总变量中仅不足3 %没有被模型解释说明; R2=0.7927表明总变量中20 %没有被模型解释说明；R2=0.7779是一个较高值且接近决定系数，这说明了模型的显著性。预测R2 和调整值R2一致。
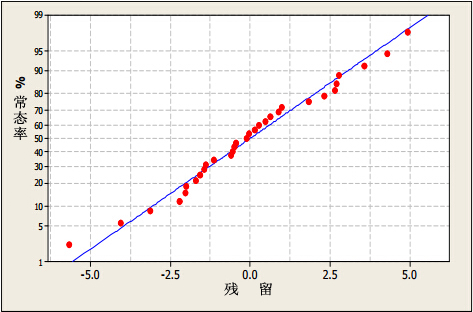
       表6中＞F值小于0.05，这说明模型比较显著；同样，砂轮速度（S）和电流（C）都有较为显著的效果。缺适性与预期的一致，不是很显著。图4为抗拉强度残留的常态率图，呈直线下降趋势，这说明误差分布正常。
4.EDDSG工艺的建模
       本论文利用ANN文献中的反向传播算法对EDDSG工艺进行建模，ANN建模分三部：训练、测定和确认；并用MATLAB软件对其进行编码。表3为实验数据训练出的ANN文献；对于网络测定，选取实验结果数目的70 %如表4所示。利用LM反向传播算法进行网络训练；LM是一种网络训练函数，该函数能够根据LM优化对权重和偏差值进行更新，由隐层的选数和每个隐层中节点的数目优化构成。
       根据网络性能对隐层数目和节点进行选择，用均方误差（MSE）对网络性能进行测试，MSE计算公式如下：


       其中，dj为jth节点的期望输出值，yj为jth节点的预测值。N为训练类型总数目，M为输出节点数目。
       表7为EDDSG工艺建模，能够预测MRR的绝对平均百分比误差（2.66%）和最大百分比误差（29.22%）。表5为RSM和ANN技术求得的实验值和预测值。图5为MRR实验值和预测值对比图。


5. RSM和ANN对比
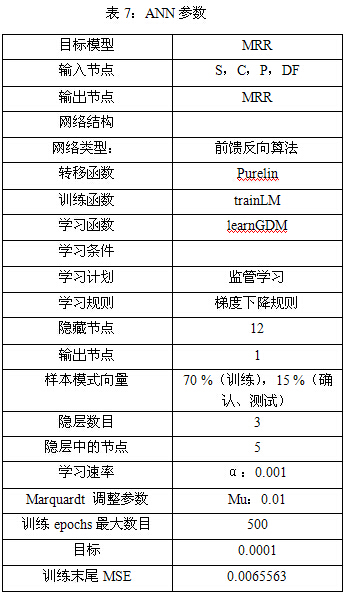
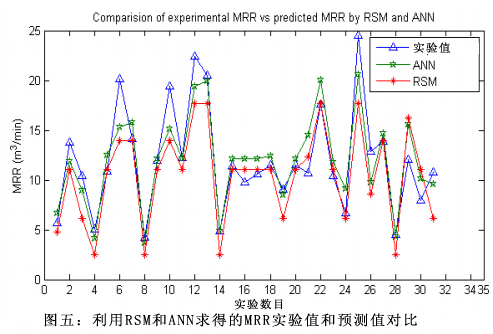
       实验将ANN模型和RSM模型的预测能力进行对比。表8为两个模型的预测值。图5为两种模型输出预测的类似对比。对于所有的输出值，ANN模型和实验值相符合，一致性很好。RSM模型的绝对偏差要比ANN模型大许多。因此，ANN模型要比RSM模型的归纳能力更强。ANN模型的这种较高的精准度主要是由于它更接近系统的非线性的能力。
6. EDDSG加工表面形态
       图6为铬镍铁合金718加工前、加工过程中在最大MRR条件下利用SEM获得的表面形态图。图6（a）中未加工表面上有浇铸痕迹和凹槽被去除的迹象并形成新生表面；此时EDDSG工艺参数为砂轮速度1200rpm，电流9 Amps，脉冲时间为150μs，占空因子为70 %。同时还观察到少数没有被磨削掉的EDM洼坑。


结论：
       1）砂轮速度对MRR影响最大，其次是脉冲速度。
       2）要获得较高的MRR值，可以将高砂轮速度、高脉冲电流、较长的脉冲时间和较大的占空因子结合起来。
       3）ANN预测模型在训练范围内可以有效预测MRR。与响应曲面模型相比，ANN模型在预测MRR值时更精确更稳定。（编译：中国超硬材料网）