摘要:本文提出了一种提高精度和缩短计算时间的方法,用于复杂刀具轨迹编程的多轴加工中心。要求复杂刀具轨迹的一些零部件有各种各样的涡轮叶片、压力泵螺旋钻和轮齿表面等。该方法依据带有浮动范围定义的样条曲线解析对拓扑结构的产生进行研究分析,还可以对多轴铣削加工工艺的特殊要求进行调整。本文提出的算法是CAD/CAM软件的基础,可用于使用任意模型的五轴加工中心和数控编程。采用高速切削的方法和定制刀具进行加工试验,结果表明,带有复杂表面的零部件数控编程时间缩短了70-80%,加工时间缩短了40-50%;充分提高了加工精度。
关键词:数控编程,多轴铣削,CAD/CAM软件,加工精度
1、引言
如今,计算机技术能充分提高编程速度,利用多种加工方法缩短零部件约90%的加工时间。但要实现复杂工件表面的高速多轴加工,则需要采用新的软件。随着更加复杂精致的产品研发,加工过程中也会出现更多技术性困难;而现有的主流算法则解决不了这些问题。例如,双曲面涡轮机叶轮工艺(图1)中,为了增大叶轮的输出力,需要双倍增加完整叶轮和截断叶轮的数量,叶轮厚度也因此而降低。据此可知,这种叶轮的实际加工时间应该双倍增加。但实际加工时间却增长了近10倍。加工一个单通道原本需要1小时,但采用全新设计的方法则需要380分钟。这是由于:
1)小直径刀具的选用和加工把进给速度由200mm/min降低到了80mm/min。
2)由于叶轮厚度变小而所需的额外加工导致材料去除较大,进而引起零件变形。
为缩短加工时间,需要实现高速切削和多轴加工的新型工艺。研发新型数控编程,提高加工精度和刀具轨迹的计算时间。

现代新型产品在精度和形状复杂度方面的提高要求CAM系统五轴加工推出新的软件。根据研究,要想提高10倍的精确度,计算时间则会增加100倍。在刀具轨迹建模中经常会出现这些问题,所以参数模型的重新计算就十分必要,而计算时间同时也很长。
将一个曲面定义为解析样条曲线的一般公式如下:
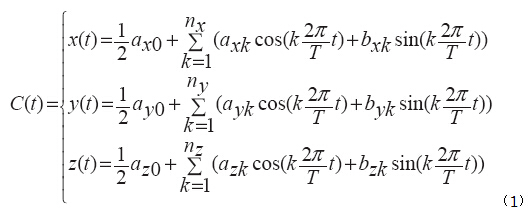
从数学模型的函数算法维护角度来分析公式1,在求得所有曲面的一般算法之后会发现,矩阵积是软件的计算机制最为便捷的方法。因子的设置,也即矢量因子a(2)和因子b(3)的矢量可以定义为:


将公式8作为所有工件模型的曲面几何参数的算法基础,可以囊括一个平行模式中所有元素的解决算法。求得矢量矩阵Cc和Sc并利用它们和矢量矩阵Ac,Bc的纯量乘法以及对矢量ac做出的修改,可以计算一个加工循环内的所有刀刃并同时计算所有加工循环内的刀刃。它可以实现计算结构Ac和Bc的制备工艺。基于u曲面和v曲面的表面表达如下:
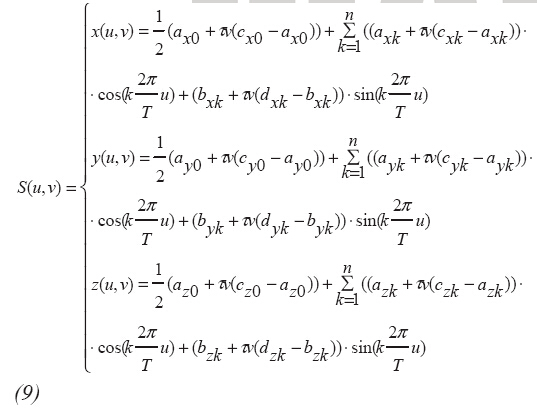
其中:
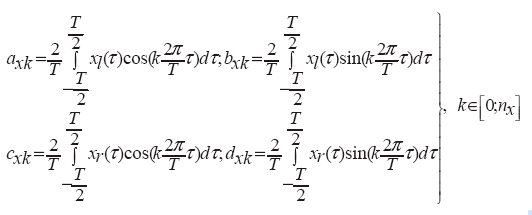
3、用于刀具轨迹计算的曲面关联的拓扑模型
刀具轨迹计算的建模集中在五轴加工工艺参数的参量问题上。在诸多金属加工工艺中五轴铣削工艺应用占比不断增大。但在不改变技术基础的前提下使用单一加工装备完成诸多加工要求则会面临一些全新的问题。这些问题归结为三大类:
1)实现最大加工速度,缩短加工时间;
2)降低加工过程中因中间环节的增多而引起的操作次数;
3)提高个性化定制产品的加工精度。
所有这些趋势在工艺计划中都应该充分的考虑到。鉴于此,创建数控编程的CAD/CAM系统应该精确地描述出工件的几何形状、在工件和刀具间相对位置上具备一定的灵活性,并考虑到切削工艺本身的一些特点。这种初始信息是加工建模的基础。
伴随复合编程T-Flex CAD/CAM10.0可以在特殊编程模块中识别类似的任务。
下面,利用复杂空间表面(SCS)工件的数控编程为例,对参数和加工进行阐述说明,如图2所示:
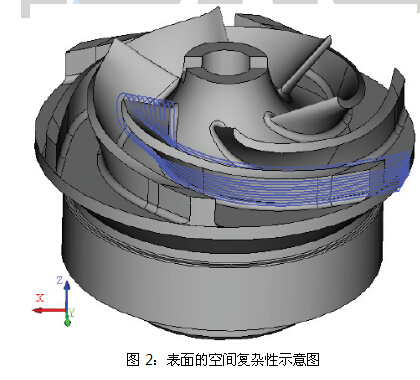
2)技术复杂性:一些零部件有表面的相对定位,会产生“阴影区”并变窄。刀具在工件表面滑动时的效应也会产生一个切削表面。鉴于此,需要设置一个刀具位置,以此来排除刀具外沿部分和其他表面的接触。
3)几何形状和技术的联合复杂性:该复杂性一方面是零部件的几何尺寸比例(如叶轮的高度和厚度比值);另一方面是基本成形表面的转换点沿加工表面产生的硬度不均匀分布。工件柔软性的不同尺寸不允许切削力保持常量,进而导致切削深度和进给等技术参数也不能保持常量。因此,有必要在数控编程过程中提供持续的变量技术参数。
T-Flex CAD/CAM系统包括专业化算法,考虑了以上特征。
参量处理的初始阶段是指形成刀具轨迹的每个表面定义的基础区的计算过程。为利用这种算法,首先需要根据限制方建立一个3D轮廓,然后再进行几何参数的数控编程。零件模型的一致性选择和规格化指导着顶部轮廓的3D轨迹并限制着底部轮廓的3D轨迹,从而使得刀具轨迹的几何组份得以定义。进一步的计算如下所示:
1)利用一致的表面内的软件将表面限制至所选方法;
2)设计一个表面的等高距,利用刀具半径求得位移;
3)求得一组刀具轨迹的闭合线圈,其中每个点沿定量组份移动,V=常量:环形或之字形;每个点以定量深度和V=V+dV的组份移动(V表示等参线)。
在加工螺旋轨迹时用该方法定义切削刀具的运动有一下优势:
1)能够实现连续定量的材料去除;
2)切削过程影响着加工时间。
由一个高度到另一个高度的辅助过渡被排除,无需对连接基础几何元素的表面进行更新。
4、五轴铣削工艺中切削刀具轨迹的计算
产生前进角的不同参量方法、产量项铣削和容许公差的参量定义等都可以归为五轴铣削的加工特性。零件的精确几何形状影响切削刀具位置的正确计算。在五轴加工中要实现设备的精确调整,需要将数控编程定位在切削刀具的中心线上。
但在机床上进行加工时,表面质量取决于切削参数和刀具的角位置。算法设计的另外一个问题就是前进刀具的角度问题,它取决于机床参数。对于T-Flex CAD/CAM系统中前进角的计算,刀具倾角有以下情况:
1)前进角设定为纵向倾角,与运动方向垂直;
2)利用聚焦法来设定刀具倾角
3)前进角为双重等距离。
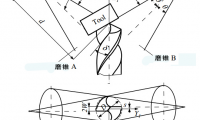
该情形下,刀具的轴在两个空间曲面的对应点上通过。
图3:设计聚焦曲面刀具轨迹的示例图
(详细内容敬请点击这里)


 手机资讯
手机资讯 官方微信
官方微信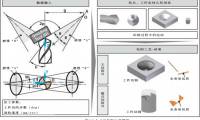









 豫公网安备41019702003646号
豫公网安备41019702003646号