关键词:田口方法,磨削,优化,循环时间,尺寸变化
1、引言
在现代化制造业领域,企业面临越来越多的挑战,特别是产品质量和产量方面,产品寿命周期缩短,成本压力增大,质量要求提高。为在国际市场保持强有力的竞争,制造企业就必须在成本效益、产品交付时间和质量等方面进行生产优化。利用CNC机床的自动化制造设备在保持高质量标准的同时能够实现较短的加工时间。
轴承制造工艺中,磨削是实现零部件要求质量和尺寸的重要工艺;而在磨削工艺中,选择进给、速度和位置等控制参数并对其进行优化对于实现最短时间内高质量性能产品的加工就非常重要。控制参数一般根据经验或手册得到,这些参数反应了零件的尺寸,椭圆度以及间接算入产品交付时间的磨削加工循环时间并最终记为单位时间的生产总量。
在选择控制参数方面,基于回归技术的数学模型需要较大的知识量和经验,而与之相比,田口方法则能够提供简单有效且系统的性能、质量和成本方面的优化设计。此外,田口方法所需实验次数少、成本低、实验时间少;而数学模型需要去做大量实验。通过设置控制参数并降低系统对变量来源的敏感性,田口方法可以优化性能特征并缩短循环时间,同时还能保持工件要求的质量。
本研究利用田口参数设计提供了一种系统的程序,借助特定的控制参数组合对圆锥滚柱轴承的外环磨削加工中的循环时间和轨道直径尺寸变化进行优化降低。实验首先介绍了田口设计方法和圆锥滚柱轴承的外环磨削加工;然后描述了利用参数设计求值并分析最佳控制参数的实验细节和实验结果;最后得出结论。
2、田口方法
田口玄一建立了一种实验设计的应用方法,包括变量属性和制造领域质量工程的经济效益。田口方法包括系统设计、参数设计和公差设计等。
对于系统设计,田口方法应用科学工程知识建立了一个基本的功能性原型设计,包括产品设计阶段和工艺设计阶段。这两个阶段涉及到了材料、零部件、参数值的选择和生产设备、试验性工艺参数值等的选择。在参数设计阶段,优化参数值以改善质量特性。有参数设计求得的最佳工艺参数值对环境和其他噪声因子引起的变量不敏感。最后利用公差设计求出最佳设置附近的公差。
由Fisher提出的实验设计方法操作比较复杂,当工艺参数增加时需要做大量实验。而田口方法则利用正交阵列的特殊设计,利用较少的实验次数来研究整个参数空间。田口玄一建议利用损失函数从预期值中求得性能特征;然后将损失函数值转化为信噪比(S/N)。在信噪比分析中通常有三种类型的性能特征:越小越好、越大越好、标准值最佳。根据信噪比分析计算求得每组工艺参数的信噪比。不考虑性能特征的类型时,较大信噪比对应较好的性能特征。因此,最佳工艺参数组就是信噪比最高的一组。另外,利用ANOVA观察哪组工艺参数具有统计显著性。借助S/N和ANOVA可以预测最佳工艺参数组合。最后通过验证实验来证实由参数设计求得的租价工艺参数。
田口方法的参数设计包括以下步骤:
·确认性能特征,选择工艺参数;
·求得工艺参数组的数量以及工艺参数间可能的交互作用;
·选择适当的正交阵列和分配至正交阵列的工艺参数;
·根据正交阵列的排列进行实验;
·计算损失函数和信噪比;
·利用信噪比和ANOVA分析实验结果;
·选择最佳工艺参数组;
·通过验证实验确认最佳工艺参数。
3、磨削工艺
对圆锥滚柱轴承外环进行内圆磨削加工,内圆磨床的基础工件如图一所示为一个工作头。除了工件和砂轮的旋转运动,内圆磨床带动砂轮在工作区做横向往返运动,同时还为砂轮-工件表面以及砂轮进给运动做反复主轴运动。工件的磨削表面受以下因素影响:
工件材料———硬质材料需要更精细的磨抛;
砂轮类型———精细磨粒磨削时的精磨效果更好;
砂轮修整———不适当的砂轮修整会损坏工件表面;
进给速度———进给速度较低时精磨效果更好;
设备刚性———陈旧设备的精整加工质量较差;
润滑清洁———对润滑剂进行过滤以去除损伤工件表面的杂质。

图一:砂轮

图二:内圆磨床

A.控制参数的选择和参数标准
图四为一个典型的磨削循环;参数选择如下:
·速度参数:
工作头主轴速度:工件的旋转轴速度rpm,表示为R142。
·位置参数:
(1)精磨循环开始时滑座的位置,表示为R104;
(2)增量后退1:精磨循环开始之前、粗磨结束之前滑座后退位置以减小环偏离,表示为R110;
(3)增量后退2:无火花磨削加工前、精磨循环结束之前滑座后退位置以减小环偏离,表示为R111。
·进给参数:
(1)空转进给速度:砂轮移至外环时空转的进给速度,表示为R127;
(2)粗进给速度1:初始粗磨阶段砂轮的进给速度,表示为R128;
(3)粗进给速度2:粗磨阶段去除材料时砂轮的进给速度,表示为R129;
以上两个粗磨阶段占材料去除量的70-80%
(4)精磨进给速度:精磨阶段砂轮的进给速度,表示为R130。

(1)无火花磨削时间:精磨之后的时间段,砂轮和工件以固定位置在外环轨迹表面最高点上旋转以去除碎屑,表示为R136;
(2)修整补偿:砂轮修整过程中被去除掉的砂轮材料量,表示为R115;
(3)修整进给速度:修整砂轮时的进给速度,表示为R132。
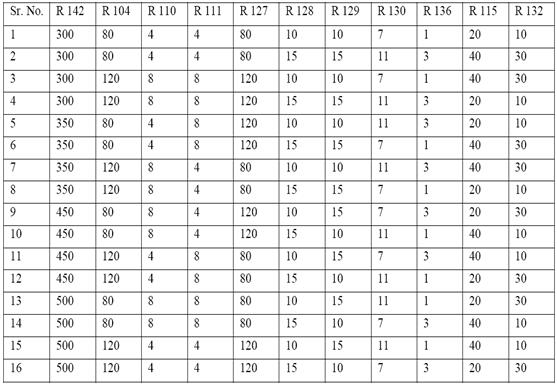
在范围值内改变控制参数,如表一所示。
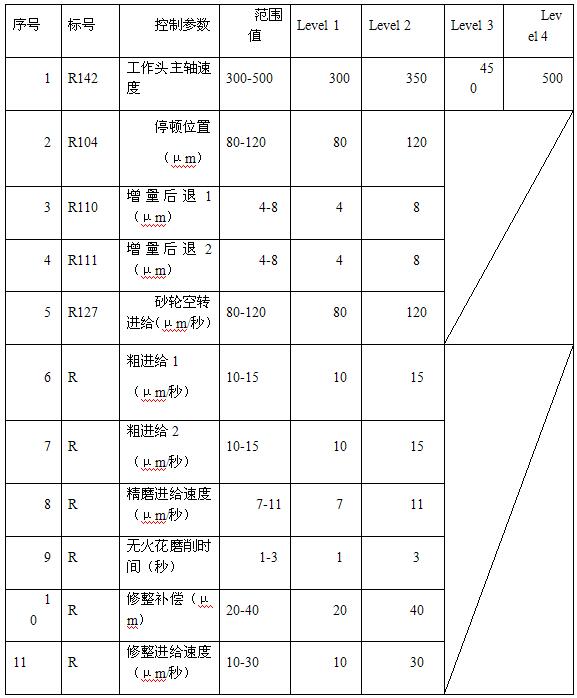

本部分讨论如何利用正交阵列减少控制参数设计优化的实验次数;利用S/N和ANOVA分析研究实验结果。根据实验结果求得控制参数的最佳设置并进行验证。
A.基线测量
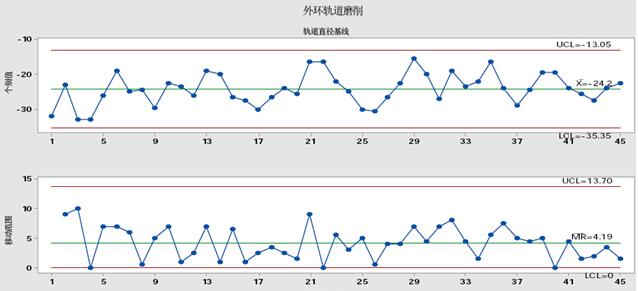
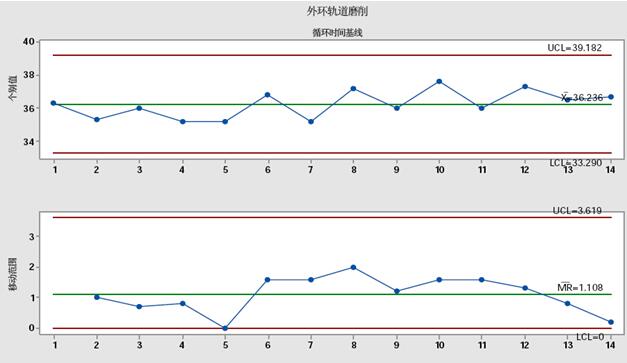
对加工过程中的磨削稳定性进行基线测量,研究发现基于I-MR图表的磨削工艺比较稳定,如图七所示为控制限制限度内的测量。23微米范围内还观察到轨道直径的平均尺寸变化;平均循环时间为36.3秒,如图八所示。基线控制参数如表二所示。

B.正交阵列实验
为选择合适的实验正交阵列,本研究采用Design-Expert MINITAB软件。根据控制参数的数量及其准级,选择L16正交阵列设计。根据所选田口实验设计进行实验,L16正交阵列如表三所示。
在田口实验法中,“信号”术语表示输出特性的所需值(平均值),“噪声”术语表示输出特性不需要的值(S.D.)。S/N比就表示平均值和S.D.的比值。田口玄一利用S/N比来测量偏离所需值的质量特性,S/N比定义为η=-10log(M.S.D.)-(1),其中M.S.D.表示输出特性的的均方差。
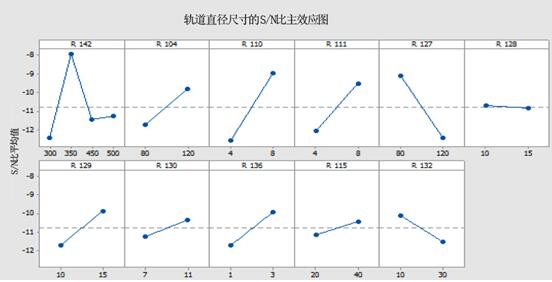 .
.利用S/N比值对外环轨道直径和循环时间的实验结果进行分析;响应图分别为图三、图四。
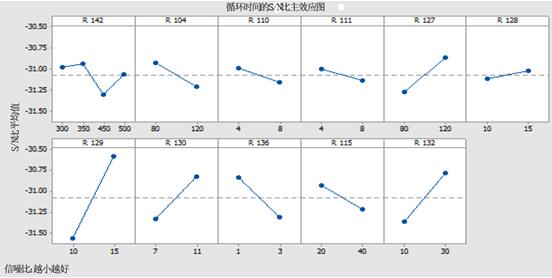
对于“标准值最佳”和“越小越好”的质量特性,不管其与否,较大的S/N比都对应着期望值附近输出特性的较小变化。对应较大的S/N比选择控制参数值以求得最佳输出结果。
D.ANOVA
ANOVA的目的是为了研究哪些工艺参数会显著影响性能特征,该目的可以通过分离S/N比的总的可变性而得。基于S/N比合计平均值的方差总和可以求得S/N比的总可变性。首先计算基于S/N比合计平均值的方差总和,SST总和分为两部分:每个设计参数所致方差综合SSd和平方误差总和SSe。每个设计参数在SST中的影响程度为SSd和SST的比值。
借助MINITAB 17软件利用ANOVA法求得工艺参数对输出响应的影响。统计上讲,以Fisher命名的F测试工具可以求得对性能特征有显著影响的工艺参数。一般情况下,F值越大,工艺参数的改变对性能特征的影响就越大。
表四为轨道直径尺寸的ANOVA结果,可以看出控制参数R142、R104、R110、R111、R127、R129、R130、R136和R132最为显著,占轨道直径尺寸总变量的96%。
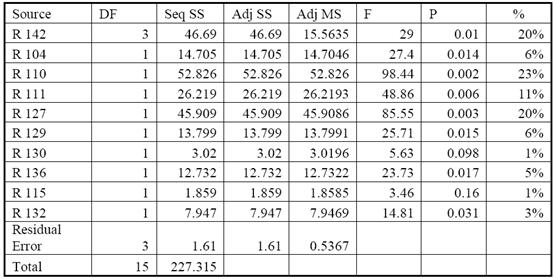
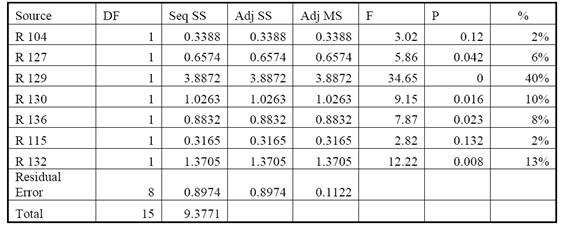
选择最佳工艺参数后便对性能特征的改善情况进行预测和确认。可以得到MINITAB 17软件求得的预测S/N比;对应的循环时间以及轨道直径尺寸分别由公式(3)、(2)求得。
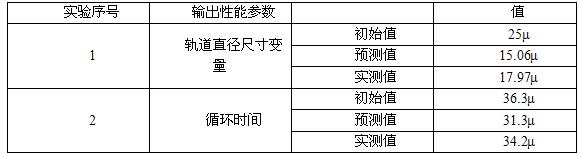
5、结论
本论文研究分析了田口方法在优化磨削工艺控制参数方面的应用。田口方法参数设计能够提供简单、系统且高效的控制参数优化方法论。实验结果证明该方法在缩短磨削工艺循环时间的同时也降低了轴承制备工艺中外环轨道直径尺寸的变化;实验求得的最佳参数通过了验证试验。下一步研究将考虑更多的因素,讨论它们是如何影响工艺的输出特性的。(编译:中国超硬材料网)


 手机资讯
手机资讯 官方微信
官方微信








 豫公网安备41019702003646号
豫公网安备41019702003646号