超硬材料网

       摘要：磨粒移动会给电镀金刚石砂轮加工工程陶瓷材料带来不利影响，降低工具寿命并影响表面粗糙度。为解决磨削过程中单颗磨粒的微切削力并提供充足的微结合力，需要将电镀结合层制备的厚度制备的足够大。但电镀结合成厚度过大又会影响磨粒的凸出性能，从而引起有效磨粒的减少。目前，制备电镀金刚石砂轮的传统方法主要是基于先验知识的反复试验法。而设计一个明确的砂轮的困难之处则在于缺少一个完整的模型来预测微粘结力和砂轮表面所有金刚石磨粒的凸出性能。本论文为单层电镀金刚石砂轮建立了一个数字砂轮模型，并数字化地模拟每个砂轮的制备程序。该模型能够提供和砂轮设计参数相关的砂轮表面、微粘结力和磨粒凸出3D示意图。根据对单颗磨粒微切削力的分析，求得最佳电镀粘结层。最后利用氧化铝工程陶瓷实验对金刚石砂轮模型的制备进行验证。
       关键词：砂轮,金刚石,陶瓷
1 引言
       氧化铝、碳化硅、氮化硅和氧化锆等工程陶瓷由于其优越的机械、化学和热性能而广泛应用于精密工程组件的制造。磨削作为工程陶瓷组件制备工艺的最后关键的一步，主要完成表面粗糙度和几何精度加工处理。而在磨削过程中，严重的磨粒脱落和磨损会导致砂轮表面的廓形误差并引起磨削表面几何形状的误差。
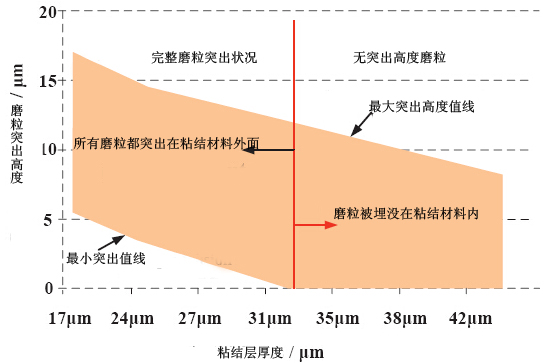
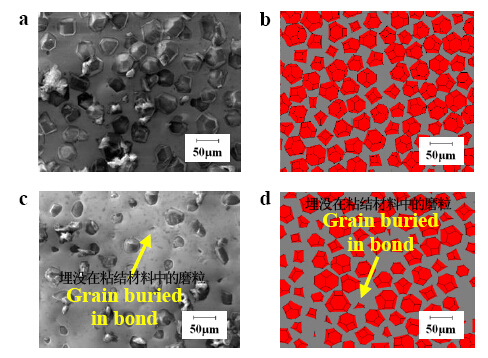
       电镀金刚石砂轮由于加工效率高、灵活性强而应用于工程陶瓷材料的磨削加工。为保证表面粗糙度和外形精度，电镀砂轮的设计必须保证有足够的磨粒突出和微结合力，如图一（a）所示。目前，设计出一个较好的砂轮仍然处于探索阶段。难点在于结合成厚度的优化。为了将微粘结力最大化，电镀层厚度需要缩小，如图一（c）所示；并由此也导致磨粒突出程度降低，切屑清理空间变小，如图一（b）所示。因此，粘结层厚度度必须控制在一个适当的范围内，以保证磨粒突出程度和足够的粘结力。

       本研究建立了一个数字砂轮模型以此来预测磨粒突出状况和磨粒微粘结力作为粘结层厚度的一个函数，考虑了金刚石形状、磨粒尺寸和粒径分布等参数。该数字砂轮模型包括砂轮形貌模型和微粘结力模型，如图二所示。据此可以量化求得最佳粘结层厚度范围，从而保证有效的微粘结力和磨粒突出。最后，利用优化过的砂轮对氧化铝工程陶瓷材料进行磨削实验，以验证模型的有效性。

2 单层砂轮表面形貌的建模算法
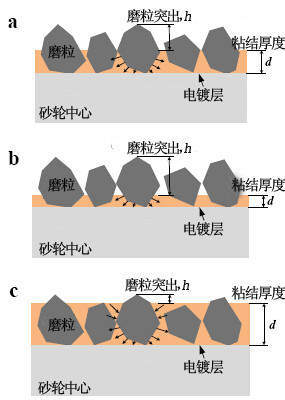
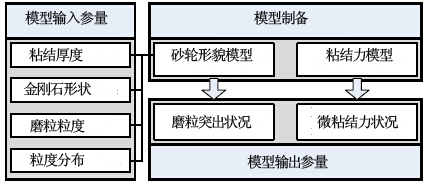
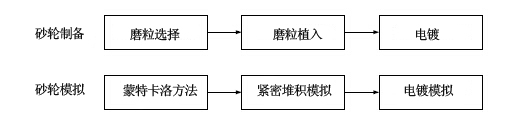
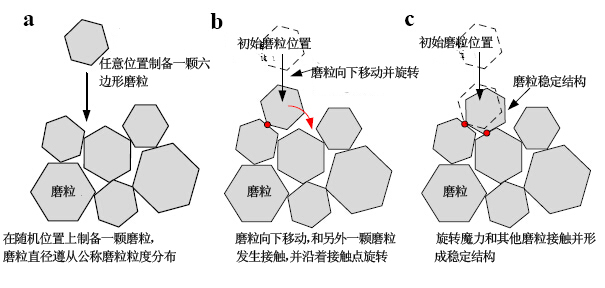
       粘结层厚度和磨粒突出状况的相关性可以由实验测量和实际砂轮模型求得。本研究根据参考文献中已有的实际砂轮模型对磨粒突出状况进行分析。砂轮建模的方法是利用数学模型来复制每个砂轮的制备步骤，包括磨粒生产、磨粒植入和电镀，如图三所示。建模既考虑了砂轮组份，如磨粒粒度、粒径分布、磨粒形状和电镀层厚度，还考虑了砂轮表面磨粒紧密堆积的机械学。图四描述了单层金刚石表面形貌模拟的紧密堆积算法。首先，在粒径分布范围内任意位置上生产出一颗六边形的金刚石磨粒，如图4（a）；然后，该磨粒开始向下移动至已存在的磨粒并和其中一个六边形磨粒接触并沿着接触点旋转，如图4（b）；最后，当该磨粒和另外的磨粒接触并形成稳定的支撑结构后，磨粒旋转停止，如图4（c）。当磨粒堆积没有空间时，该步骤停止，在砂轮中心形成最终的致密堆积。

图三：砂轮形貌模型的模拟步骤

图四：（a）初始随机位置上制备一颗六边形的磨粒；（b）该磨粒向下移动并和另外一颗六边形磨粒接触；（c）磨粒旋转并和另外一颗磨粒接触并形成稳定结构

图五：（a）金刚石磨粒（b）测量的砂轮（c）建模砂轮

       图五为测量砂轮和建模砂轮的表面形貌对比图；5（b）为电镀砂轮（800/100）测量（磨粒形状如图5a所示）。5（c）为建模金刚石砂轮表面。建模砂轮和测量结果的对比有着显著的相似之处。
       除了直接的肉眼可观察的对比外，模拟结果和实验测量结果在磨粒突出高度值上也进行了对比。对磨粒大小为341.2μm、213.8μm和138.2μm的金刚石砂轮的磨粒突出状况进行测量和模拟。利用Keyence VK-X100白光显微镜对砂轮表面进行测量。如图六（a）所示，从测量粒度的峰值中提取横截面。横截面轮廓的峰值和谷值之间的差别和磨粒突出的高度相关，如图六（b）所示。图7为磨粒突出高度分布对比图，可以看出模拟和实验测量得到的磨粒突出平均值和分布范围之间的误差接近50%左右。

图六：（a）砂轮形貌测量（b）磨粒突出高度测量

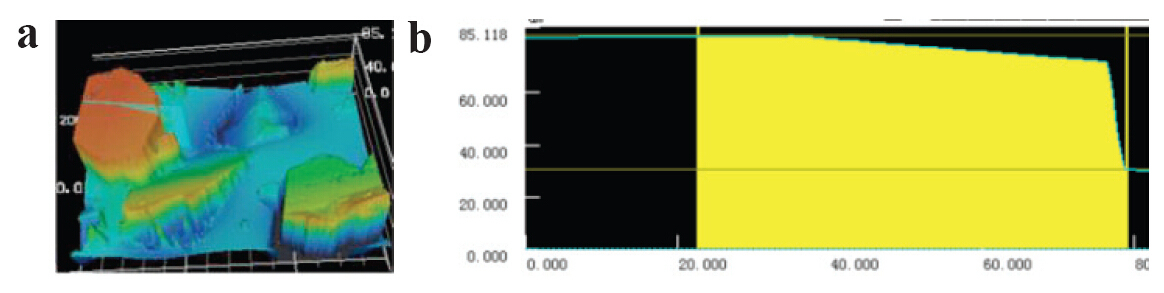
图七：实验测量和模拟中的磨粒突出高度对比

 

       在磨削工艺中，微粘结力的定义为利用粘结层把持磨粒位置以此来克服微切削力的最大力。单颗磨粒的微粘结力受晶粒取向、粘结厚度和粘结机械性能的影响。为建立微粘结力和晶粒取向以及粘结厚度之间的关联，实验为粘结-磨粒界面建立了一个有限元素模型，如图8所示。此外，利用单颗磨粒脱离实验来验证微粘结力模型的精度。

图八：（a）FEM模型；（b）FEM模型结果
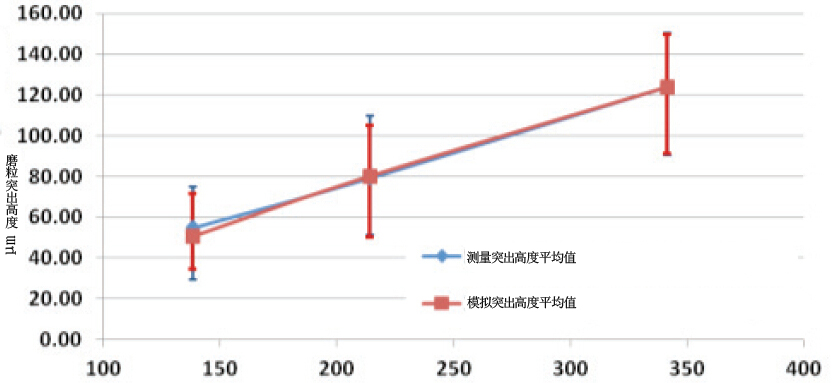
图九：（a）金刚石磨粒；（b）磨粒夹持；（c）单颗磨粒嵌入
图十：（a）实验结构图；（b）工具移动过程中的力信号

       在有限元素模型中，利用Keyence VHX-500F显微镜对金刚石磨粒的尺寸和取向进行测量。粘结剂的抗屈强度和弹性模量由MTS XP 纳米压痕仪测得；图九、十为单颗磨粒脱离实验装置。为测量微粘结力，将一颗金刚石磨粒放置在平台上，用规定厚度的电镀Ni-Co合金粘合，如图九所示。将单颗磨粒工具放置在数控机床上进行外斜面螺纹车削试验，如图10（a）所示。10（b）中红色曲线为切割深度从0μm增大到15μm时的工具横向进给。绿色曲线为测量所得粘结力，相当于磨粒从磨粒夹持上脱落时的最大切割力。
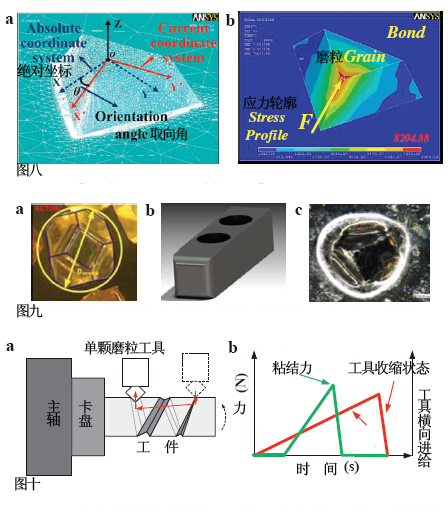
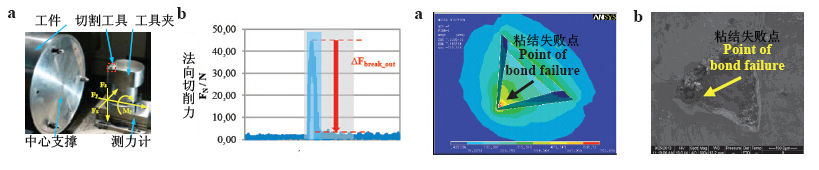
       为保证切割进程中的精度，实验使用2μm高精度数控机床，如图11（a）所示。单颗磨粒切割工具固定在测力计顶部（测力计精度0.01N）。模拟和实验中的磨粒脱落对比如图12所示。可以看出磨粒和粘结剂界面角落处由于粘结材料的无效而导致磨粒脱落。

       为验证有限元素模型的有效性，利用100μm、150μm、200μm和250μm粘结层厚度进行实验，以对比模拟结果。图13为模拟结果和实验结果对比，验证了模型的有效精度，平均误差在15%。
4 无磨粒脱落砂轮的制备
       为制备工程陶瓷材料磨削工艺用无磨粒脱落砂轮，粘结层厚度的设计必须满足以下条件：1）所有磨粒最小粘结力必须大于最大微切割力（见公式1）；2）所有磨粒突出高度必须大于0（见公式2）；任意磨粒的微切割力在0N-5N之间变化。
       Fb(Gi)＞Fc(Gi) (1)
       h(Gi)＞0 (2)
       本论文中，砂轮所用磨粒材料为＃375金刚石磨粒，3.6μm标准误差。磨粒形状为六边形，有6个方形面和12个六边形面构成。为验证粘结厚度的最佳范围值，分别利用17、24、31、38μm厚度进行实验。粘结层材料为原子比为3:1的Ni-Co合金。表二为砂轮形貌模型和粘结力模型的模拟参数。

表二：砂轮优化设计的模拟参数

图14：最大粘结厚度计算

       图14描述了不同粘结厚度值的磨粒突出高度变化，对于每一个粘结厚度值，最大、最小突出高度值都由模拟算得。可以清晰地观察到，当粘结厚度值为33μm时，粘结层下的金刚石磨粒开始粉碎。这说明砂轮中心过多的粘结材料导致磨料不足，不足以去除工件材料。因此，为确保完整的磨粒突出，最大粘结厚度可以调整到33μm。
       在粘结层厚度值周期内，为合成微粘结力范围，研究利用反应曲面分类研究法(RSM)研究多输入变量对性能指标和质量特性的潜在影响。因此，预期输出指标可以表达为输入工艺参数（晶粒取向、粘结层厚度）的一个多项式函数，如公式3所示。由工艺参数组成的函数叫做响应面。对于所有预测变量，通常利用二阶模型求得多项式近似值，如公式4所示。在所有预测变量中，OA和TOB为磨粒取向角度和粘结层厚度。Fbonding为对应条件的粘结力。对于模型回归程序，研究利用最小二乘法，如公式5所示。
       Fbonding＝f(x1,x2)＝f(OA,TOB) （3）
       y＝bo＋ （4）
       S(θ)＝ （5）
       其中，OA为取向角度，TOB为粘结层厚度。
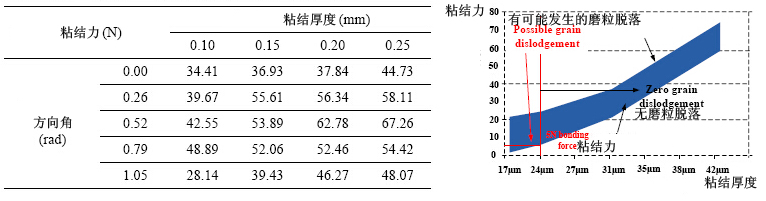
       考虑到磨粒的对称特性，分别选择0°、16°、30°、45°和60°的取向角。粘结层厚度选择17μm、24μm、31μm和38μm，涵盖了磨粒直径的36.2%到80.9%。表三为所有条件下的模拟结果。回归模型如公式6所示。对于每一个粘结厚度值，可以根据回归公式计算最大粘结力和最小粘结力。对最大、最小粘结力进行排列，可以求得粘结层厚度值范围内的微粘结力周期。
       通过将5N设置为最小粘结力的临界值可以推断出最小粘结层厚度必须大于24μm才能够降低磨削工艺中磨粒脱落的可能性，如图15所示。

       Fbonding＝43.8＋18.0×OA－3200.3×TOB－29.6×OA2＋88980.1×TOB2 ＋473.9×OA×TOB （6）
       对磨粒突出情况的研究以及微粘结力变量作为粘结层厚度值的一个函数有助于电镀金刚石砂轮的优化设计参数。为保证100%的磨粒突出，粘结厚度不能大于33μm；为克服磨削工艺中的微切削力，粘结厚度值不低于24μm。图16中，将两个范围值叠加可以求得粘结层厚度值的最佳范围值，在24μm~33μm之间。

5 实验证明
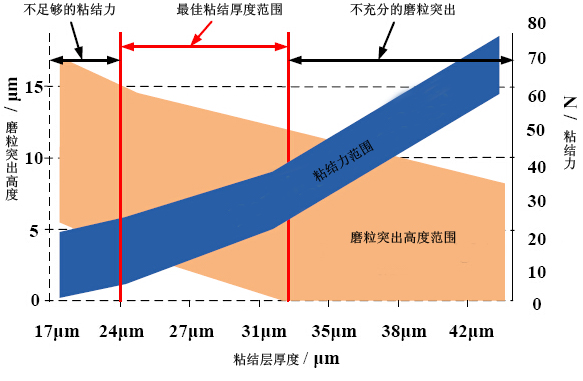
       为验证砂轮最佳设计方法的有效性，实验制备了三种粘结层厚度不同的砂轮用于磨削试验，参数如表四所示。根据上述研究，37μm粘结层厚度的砂轮C的磨粒突出程度不能达到100%；21μm粘结层厚度的砂轮A不能有足够的微粘结力；30μm粘结层厚度的砂轮B在磨粒突出和无磨粒脱落方面要稍有缺陷。

       实验采用的工件材料为氧化铝工程陶瓷材料，莫氏硬度为9。表五为平面磨削工艺参数，通过求得工件的表面粗糙度和砂轮表面状况对磨削质量进行表征。

       在进行磨削加工前对砂轮的表面形貌进行测量和模拟以便获得砂轮B和砂轮C的磨粒突出状况，如图18所示。图18（a、b）显示砂轮B的磨粒完全突出在粘结材料外面；图18（c、d）显示砂轮C的部分磨粒由于粘结层厚度过大而被埋没在粘结材料里面。

6 结论
       本研究建立了一种制备电镀砂轮的数字设计方法。结论如下：（1）该方法能够将砂轮设计的关键参数（磨粒尺寸、尺寸分布、粘结厚度等）和砂轮性能（磨粒突出状况、微粘结力）关联起来。（2）本研究建立了粘结厚度和磨粒突出、微粘结力之间的综合关联性。3.6μm粒度分布的＃375金刚石砂轮的最佳粘结层厚度为24μm~33μm。（3）氧化铝工程陶瓷材料的磨削实验验证了数字砂轮设计方法的有效性。(编译：中国超硬材料网)