摘要 摘要:在20-400开氏度范围内对掺硼单晶HPHT人造金刚石(BDD)和高纯IIa型人造金刚石进行对比研究。BDD中掺硼浓度约1019cm-3,为功率器件设备中p+衬底材料的浓度代...
摘要:在20-400开氏度范围内对掺硼单晶HPHT人造金刚石(BDD)和高纯IIa型人造金刚石进行对比研究。BDD中掺硼浓度约1019cm-3,为功率器件设备中p+衬底材料的浓度代表值。在100开氏度左右,BDD热导率低于IIa型金刚石热导率的10倍左右,但是超过室温条件下,该差值低于30%。实验观察得到的偏差主要由高浓度掺硼人造金刚石的扩展性结构缺陷所发生的声子散射所致。
引言:
金刚石材料具有硬度高、光学透明度好、热导率高的卓越性能。在100K温度左右热导率高达10000W/(m.K),在室温下热导率高达2500 W/(m.K)。目前,人造单晶金刚石广泛应用在光学、X射线、光电子和电子设备中。尤其是高纯IIa型人造金刚石,是高功率短波自由电子激光设备中X射线反射镜的绝佳材料。而掺硼IIb型人造金刚石(BDD)则是用于高功率高频高温电子设备的典型P型半导体材料。在以上两种设备领域,热导率是影响设备设计的关键参数,而对于BDD热导率的研究目前则比较少。
金刚石热导率的早期研究主要在1911-1953年间,主要对杂质密度未经处理的天然金刚石的热导率进行研究。1990-1993年间,不少学者对人造金刚石的热导率进行了大量研究;主要是在不同同位素含量条件下研究人造金刚石热导率和温度的关系。实验数据经过Debye-Callaway模型框架分析,得出结论:高纯金刚石的热导率主要手碳同位素原子的声子散射影响。在热导率的研究中主要考虑了两种截然不同的方法:不予考虑声子-声子散射的正规过程;假定存在正规过程的支配控制。Wei等人通过设定一个系数来计算求得声子-声子散射的正规过程的影响并使其与100-1000开氏度范围内热导率-温度关系相拟合。
本研究对高纯单晶人造金刚石和掺硼金刚石在20-400开氏度温度范围内的热导率进行了对比实验研究。BDD中掺硼浓度满足各类电子设备p+金刚石衬底材料代表值的要求。在温度低于100开氏度和高于室温时虽然实验数据略有偏差,但掺硼BDD热导率仍然比其他宽带隙半导体材料的热导率要高,且仅比高纯人造金刚石的热导率低30%左右。研究对影响IIa型和IIb型金刚石声子散射过程的差异因素进行了分析。
实验设计
利用量子物理性质测量设计系统(QD PPMS)和EverCool2密闭循环低温恒温器并采用稳态法对热导率进行测量。PPMS系统在1.8-400开氏度温度范围可以实现高真空测量(<10-5Torr),温度误差仅0.05开氏度。
根据稳态法可知,当通过试样的热流为常量时,试样一端的热功率和试样两端的温差ΔT成比例关系,如下所示:
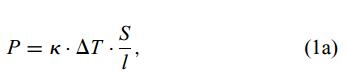
其中,l为试样长度,S为横截面积,k为热导率。
稳态法的基本工作原理如图一所示。对一个试样的一端进行加热,另一端连接恒温槽。测量得到试样两端的温度和常量温差,并根据公式1a计算热导率。
引言:
金刚石材料具有硬度高、光学透明度好、热导率高的卓越性能。在100K温度左右热导率高达10000W/(m.K),在室温下热导率高达2500 W/(m.K)。目前,人造单晶金刚石广泛应用在光学、X射线、光电子和电子设备中。尤其是高纯IIa型人造金刚石,是高功率短波自由电子激光设备中X射线反射镜的绝佳材料。而掺硼IIb型人造金刚石(BDD)则是用于高功率高频高温电子设备的典型P型半导体材料。在以上两种设备领域,热导率是影响设备设计的关键参数,而对于BDD热导率的研究目前则比较少。
金刚石热导率的早期研究主要在1911-1953年间,主要对杂质密度未经处理的天然金刚石的热导率进行研究。1990-1993年间,不少学者对人造金刚石的热导率进行了大量研究;主要是在不同同位素含量条件下研究人造金刚石热导率和温度的关系。实验数据经过Debye-Callaway模型框架分析,得出结论:高纯金刚石的热导率主要手碳同位素原子的声子散射影响。在热导率的研究中主要考虑了两种截然不同的方法:不予考虑声子-声子散射的正规过程;假定存在正规过程的支配控制。Wei等人通过设定一个系数来计算求得声子-声子散射的正规过程的影响并使其与100-1000开氏度范围内热导率-温度关系相拟合。
本研究对高纯单晶人造金刚石和掺硼金刚石在20-400开氏度温度范围内的热导率进行了对比实验研究。BDD中掺硼浓度满足各类电子设备p+金刚石衬底材料代表值的要求。在温度低于100开氏度和高于室温时虽然实验数据略有偏差,但掺硼BDD热导率仍然比其他宽带隙半导体材料的热导率要高,且仅比高纯人造金刚石的热导率低30%左右。研究对影响IIa型和IIb型金刚石声子散射过程的差异因素进行了分析。
实验设计
利用量子物理性质测量设计系统(QD PPMS)和EverCool2密闭循环低温恒温器并采用稳态法对热导率进行测量。PPMS系统在1.8-400开氏度温度范围可以实现高真空测量(<10-5Torr),温度误差仅0.05开氏度。
根据稳态法可知,当通过试样的热流为常量时,试样一端的热功率和试样两端的温差ΔT成比例关系,如下所示:
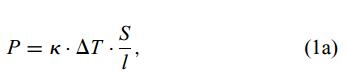
其中,l为试样长度,S为横截面积,k为热导率。
稳态法的基本工作原理如图一所示。对一个试样的一端进行加热,另一端连接恒温槽。测量得到试样两端的温度和常量温差,并根据公式1a计算热导率。
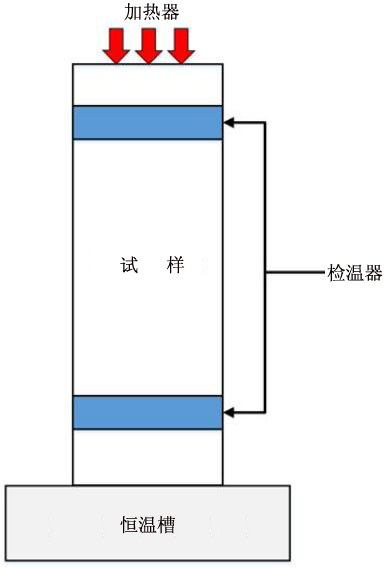
图一:稳态法基本工作原理
利用该方法计算热导率时需要得到试样的几何尺寸。在本研究的实验中,我们对试样的宽度进行估算以便得到较为明显的温差。试样的长度限制在晶粒大小(l=3mm),试样厚度要足够小(d=100μm)。根据公式1a,试样的宽度a可以如下所表示:

其中,金刚石预估最大热导率为15000 W/(m.K),可用加热器功率为50mW,温差为0.5开氏度。据此可求得宽度a为0.2mm。
试样制备
利用温度梯度法在高温高压条件(5.5GPa、1440℃)下在“螺旋环形”高压装置内制备出人造单晶金刚石。所用溶媒合金为Fe-Al-C合金(91:5:4 wt%)。溶剂中添加铝作为除氮剂。碳源为高纯石墨(99.9995%)。
在碳源中添加0.5at%的无定形硼用于IIb型金刚石生长;根据红外光谱观测,生成的BDD晶体中的硼浓度约1019cm-3(~20ppm)。这种掺杂晶体的电子属性和生长问题在本文参考文献中详细说明。
利用激光将生长出的金刚石晶体切成成片,并对其进行机械打磨抛光,金刚石片厚度约100μm。利用CVD法在BDD片上生长出绝缘IIa型金刚石薄层(~10μm),用于电绝缘(如图二)。利用仲烷基磺酸钠、丙酮和异丙醇对金刚石片进行化学清洗,然后在680℃下对其进行热处理,以去除金刚石片上的污渍并防止表面发生氢导电性。
试样制备
利用温度梯度法在高温高压条件(5.5GPa、1440℃)下在“螺旋环形”高压装置内制备出人造单晶金刚石。所用溶媒合金为Fe-Al-C合金(91:5:4 wt%)。溶剂中添加铝作为除氮剂。碳源为高纯石墨(99.9995%)。
在碳源中添加0.5at%的无定形硼用于IIb型金刚石生长;根据红外光谱观测,生成的BDD晶体中的硼浓度约1019cm-3(~20ppm)。这种掺杂晶体的电子属性和生长问题在本文参考文献中详细说明。
利用激光将生长出的金刚石晶体切成成片,并对其进行机械打磨抛光,金刚石片厚度约100μm。利用CVD法在BDD片上生长出绝缘IIa型金刚石薄层(~10μm),用于电绝缘(如图二)。利用仲烷基磺酸钠、丙酮和异丙醇对金刚石片进行化学清洗,然后在680℃下对其进行热处理,以去除金刚石片上的污渍并防止表面发生氢导电性。
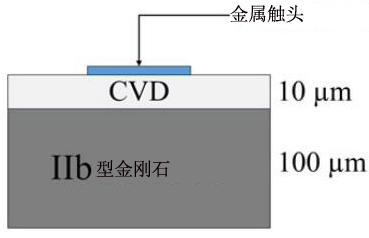
图二:生长出CVD金刚石层后的试样横截面
利用剥离光刻和磁控溅射工艺沉积出三个1kΩ的铂电阻,其中两个电阻用作试样冷热两侧的测温器,另一个用作电阻加热器以提供热脉冲。利用激光切割出宽0.3mm长3mm的热传导试样尺寸(如图三)。利用热导率较高的特制环氧树脂将试样固定在标准PPMS试样球上以提供较好的热接触。这种试样球可以为测温器和加热器提供良好的导电连接,同时还能充当恒温槽。导电连接有40μm后的金线来完成(如图四)。
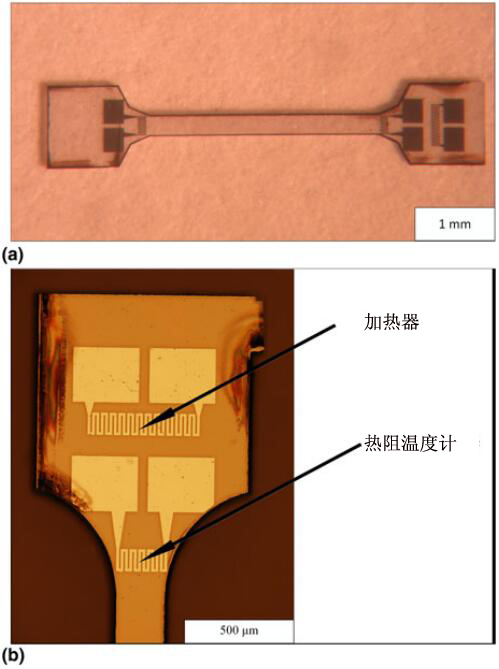
图三:(a)带有测温器和加热器的试样;(b)加热器和测温器的放大示意图

图四:固定在试样球上的试样示意图
实验结果和分析
图五为试样的实验数据。可以看出,IIa型金刚石在室温下的热导率为2500 W/(m.K),和已知实验数据接近。在90开氏度时最大热导率达到17000 W/(m.K)以上。在150开氏度以下,IIa型金刚石的热导率是BDD热导率的10倍,但在高于300开氏度温度时两者温差仅30%左右。
图五为试样的实验数据。可以看出,IIa型金刚石在室温下的热导率为2500 W/(m.K),和已知实验数据接近。在90开氏度时最大热导率达到17000 W/(m.K)以上。在150开氏度以下,IIa型金刚石的热导率是BDD热导率的10倍,但在高于300开氏度温度时两者温差仅30%左右。
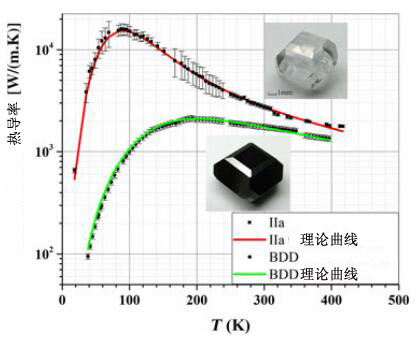
图五:BDD金刚石和高纯IIa型金刚石的实验数据
图六为IIa型金刚石热导率和温度关系的最佳匹配理论曲线,它可以解释声子散射的不同机制。利用改进后的Callaway模型框架范围内的最佳匹配可以计算出热导率和温度的关系。
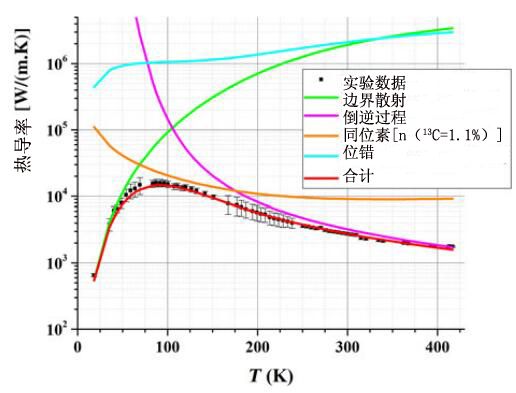
图六:IIa型金刚石热导率的测量值和计算值;声子散射的不同过程的影响
在低于德拜温度(≈1900开氏度)条件下,电荷载体密度较低的材料的热输送通过声频声子得以实现。绝缘体和半导体由于非弹性声子散射而产生热阻率。我们对点缺陷、扩展缺陷(位错)和晶体边界上不同类型的非弹性声子散射如声子-声子散射进行了讨论(置换原子和同位素),Callaway模型假定声子散射进程互不影响,且存在不同的具体时间τi。那么,总散射时间τ表达如下:

本研究中,每一进程的散射时间采用以下表达式。对于正规过程:
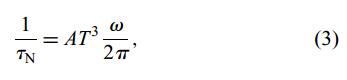
其中,A为温度无关参数,T为温度,ω为声子频率。对于倒逆过程:
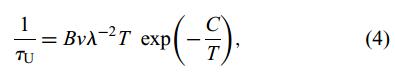
其中,B和C为温度无关参数,λ为声子波长度,v为材料的平均声速。对于边界散射:

其中,d为试样尺寸参数。
对于点缺陷,我们考虑采用同位素置换的办法:
对于点缺陷,我们考虑采用同位素置换的办法:
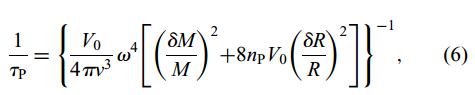
M为晶体的原子质量;δM为置换原子和溶剂原子的质量差;R和δR分别为溶剂原子的半径,置换原子和溶剂原子的半径差值;V0为每个原子的体积;np为点缺陷密度。公式的第一项为原子质量差值,第二项为镀附引起的晶格变形。在同位素置换中,第二项为0。
在扩展结构性缺陷的声子散射中,有两个因素需要考虑:晶格缺陷的散射和弹性场的散射。
下述为散射次数的表达式:
在扩展结构性缺陷的声子散射中,有两个因素需要考虑:晶格缺陷的散射和弹性场的散射。
下述为散射次数的表达式:
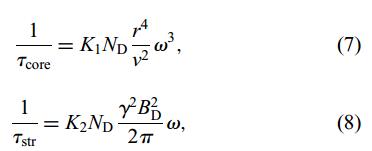
其中,k1和k2为温度无关参数,ND为差排密度;BD为位错伯格斯矢量,r为位错半径,γ为格留乃森参数。
根据公式(3)-(8)计算热导率和温度的关系,如图6所示。每条曲线代表一种情形下的热导率。图6说明了声子散射过程在一定温度范围内的影响。X射线衍射研究表明以TISNCM法生长出的IIa型金刚石的位错密度较低,因此它们对热导率应该不会有什么影响。
低温条件下热导率最大值的位置和高度由两种过程计算而得:声子边界散射和同位素13C原子散射。在T>200开氏度时,热导率受倒逆过程影响且200-300开氏度范围内散射对13C同位素的影响较弱。将该数据范围和理论模型相拟合可以求得公式3、4中A和B的值。我们选择参量C=670K作为中值,因为它对最终计算结果的影响较小。表一为拟合参量优化值。
图7为BDD的实验结果和理论曲线。在整个温度范围内理论曲线和实验数据的拟合较好。IIb型金刚石的热导率在190开氏度处达到最大值2100W/(m•K),比高纯金刚石热导率低了很多。然而BDD在室温条件下拥有相对1600W/(m•K)的较高热导率,且它和IIa型金刚石热导率的差值低于30%。
根据公式(3)-(8)计算热导率和温度的关系,如图6所示。每条曲线代表一种情形下的热导率。图6说明了声子散射过程在一定温度范围内的影响。X射线衍射研究表明以TISNCM法生长出的IIa型金刚石的位错密度较低,因此它们对热导率应该不会有什么影响。
低温条件下热导率最大值的位置和高度由两种过程计算而得:声子边界散射和同位素13C原子散射。在T>200开氏度时,热导率受倒逆过程影响且200-300开氏度范围内散射对13C同位素的影响较弱。将该数据范围和理论模型相拟合可以求得公式3、4中A和B的值。我们选择参量C=670K作为中值,因为它对最终计算结果的影响较小。表一为拟合参量优化值。
图7为BDD的实验结果和理论曲线。在整个温度范围内理论曲线和实验数据的拟合较好。IIb型金刚石的热导率在190开氏度处达到最大值2100W/(m•K),比高纯金刚石热导率低了很多。然而BDD在室温条件下拥有相对1600W/(m•K)的较高热导率,且它和IIa型金刚石热导率的差值低于30%。
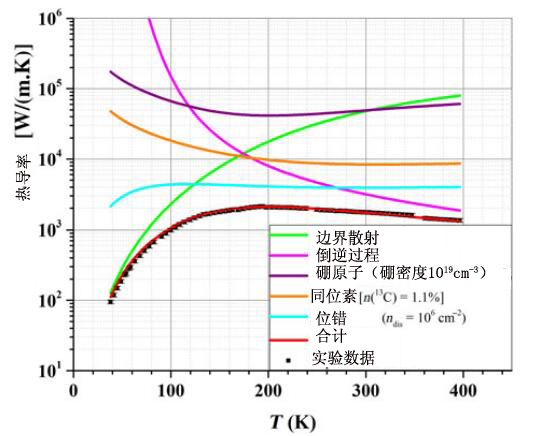
图七:BDD的实验结果和理论曲线;声子散射的不同过程的影响
在BDD实验中,我们利用公式6对密度为1019cm-3的置换硼原子声子散射的附加过程进行表述说明。差排密度106cm-2主要来自X射线衍射形貌,且在Callaway模型框架内拟合较好。

表一:来自本研究中最佳拟合和文献中的模型参数值
按照我们在T>300开氏度条件下得到的实验结果,倒逆过程对BDD的热导率的影响较大,这一点和IIa型金刚石实验类似。但BDD热导率最大值受位错散射的限制而非同位素杂质的限制。在整个温度范围内,掺杂金刚石的热导率基本不受单一置换硼原子的影响。但是掺杂含量的提高会引起BDD形貌因晶格应变松弛而发生扩展性结构缺陷。
结论
研究在20-400开氏度温度范围内对IIa型单晶高纯金刚石和BDD金刚石的热导率进行对比研究。结果表明在高于室温条件下,声子-声子散射对两种类型的金刚石热导率都有影响。在T>300开氏度条件下IIa型和IIb型金刚石热导率的差值大小低于30%。
低温条件下BDD热导率最大值受结构缺陷散射的影响,而非同位素杂质的影响(主要针对IIa型金刚石实验)。和IIa型金刚石相比,BDD热导率在T<140开氏度条件下出现急剧下降。根据该温度范围内的数据分析,扩展性结构缺陷上的声子散射对BDD热导率的影响要远大于散射对置换硼原子的影响。(编译:中国超硬材料网)
结论
研究在20-400开氏度温度范围内对IIa型单晶高纯金刚石和BDD金刚石的热导率进行对比研究。结果表明在高于室温条件下,声子-声子散射对两种类型的金刚石热导率都有影响。在T>300开氏度条件下IIa型和IIb型金刚石热导率的差值大小低于30%。
低温条件下BDD热导率最大值受结构缺陷散射的影响,而非同位素杂质的影响(主要针对IIa型金刚石实验)。和IIa型金刚石相比,BDD热导率在T<140开氏度条件下出现急剧下降。根据该温度范围内的数据分析,扩展性结构缺陷上的声子散射对BDD热导率的影响要远大于散射对置换硼原子的影响。(编译:中国超硬材料网)


 手机资讯
手机资讯 官方微信
官方微信










 豫公网安备41019702003646号
豫公网安备41019702003646号