超硬材料网

       本期论文成果介绍体金刚石在单轴应变下的异常热响应金刚石材料具有超高的导热系数，并对应力具有敏感的热响应，是嵌入式冷却模式中理想的热沉材料。近日哈尔滨工业大学红外薄膜与晶体团队通过第一性原理方法预测了块体金刚石应力-热导率依赖关系，并在小尺度应变作用下发现了金刚石热导率的异常增加。此工作发表在《PHYSICAL REVIEW B》，题目为Anomalous thermal response of bulk diamond to uniaxial (100) strain: A first-principles prediction。

       论文信息

       王彪, 赵继文, 胡彦伟, 何玉荣, Nikolay Rodionov, 韩杰才, 朱嘉琦*

       https://doi.org/10.1103/PhysRevB.106.184303

       通讯作者：朱嘉琦教授

       研究背景

       金刚石是一种由碳元素组成的晶体材料，具有极高的导热系数。这得益于其超高的声速和较弱的声子倒逆散射。随着电子元器件集成化、小型化和性能的迅速提高，其功率密度也越来越高。嵌入式冷却是第三代热管理技术，在嵌入式冷却模式中，金刚石已经成为一种理想的散热材料。目前，微波等离子体辅助化学气相沉积[1]和高温高压方法[2]被用于金刚石的生产。Ralchenko等人制备了高纯合成单晶金刚石(天然碳同位素组成)，在室温下表现出最高的κ值，为2400 W m-1 K-1[3]。就导热性而言，金刚石是天然材料的天花板。然而，是不是有可能超过这一热导率(κ)极限呢？应变是调整金刚石物理性能的有效工具。通过施加应力改变金刚石的晶格和碳核周围电子的分布，可以获得金刚石的反常物理性质。Dang等人[4]在室温单轴拉伸载荷下实现了微加工金刚石样品范围内的均匀弹性应变。Liu等人[5]预测了压缩剪切应变金刚石晶体中的超导现象。此外，Broido等人[6]发现，在400 GPa的高静水压力下，金刚石的导热系数提高了近5倍。因此，进一步探讨应变工程对金刚石κ的影响具有相当大的科学价值和工程指导意义。

       研究内容

       本文利用声子玻尔兹曼输运方程的第一性原理计算，预测了金刚石沿<100>晶向在三个尺度应变（0.1%、1%和10.5%下）的κ变化。首先利用密度泛函理论预测了金刚石的应力应变依赖性和非应变金刚石的κ温度依赖性，如图1。预测结果与实验结果吻合较好。计算的单轴应变-热导率依赖关系表明，由于非谐原子间相互作用的减弱，金刚石的κ在小尺度单轴应变下异常增加了约15%。在大尺度应变下，由于声子群速度的降低和声子散射通道数量的增加，κ显著降低。

图1 金刚石应力应变依赖关系

       图2为不同尺度下单轴拉应力下金刚石κ的温度依赖性。单轴应力的应用并没有改变金刚石κ的温度依赖性。在高温下，声子-声子散射提供了大部分热阻。在这种状态下，温度的升高增加了所有频率下声子的热占用，导致本征三声子散射率增大，κ变小。从图中可以观察到在单轴应变作用下的异常响应：κ随小尺度应变增大，随大尺度应变减小。图2的插图表明，在各向同性拉伸下没有观察到这种现象。这种行为通常在拉伸的二维材料中观察到，一般是热容、群速度和声子寿命协同作用的结果。但0.1%的小尺度应变对声子色散影响微乎其微的体金刚石材料来说，这种热响应是异常的。在室温下，κ最高可增加15%。在100K的低温下，反应更明显，κ可提高约36%。这种应变-热导依赖性的跨尺度比较和分析被大多数研究忽略了。

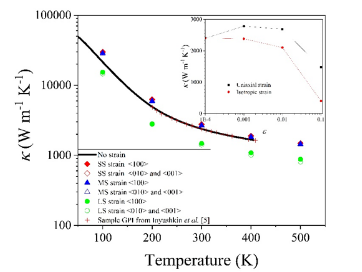
图2 单轴拉应力下金刚石热导率的温度依赖性

       图3 (a)和(b)分别给出的声子平均自由程（MFP）和声子寿命表明，它们的变化规律与κ的变化规律相似。小尺度和中尺度应变增加了声子MFP和寿命，大尺度应变则明显降低了声子MFP和寿命。因此，应变对κ的影响主要是通过影响声子散射率。图3(b)插图显示了小尺度应变对N和U散射的影响。小尺度应变对U和N散射均有抑制作用，但对同位素杂质散射几乎无影响。此外，我们的计算表明，SS应变大大减少了低温下N散射；此外，小尺度应变对长MFP声子的影响很大，如图3(a)所示。

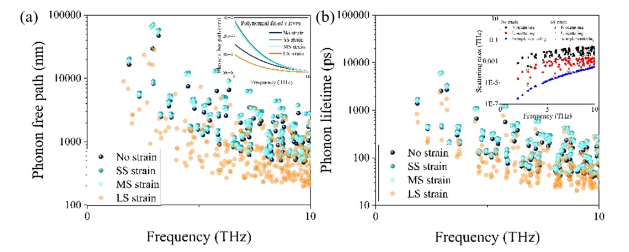
图3 应力依赖关系：(a)声子平均自由程(图中为相应的多项式拟合曲线)和(b)声子寿命(图中为SS应变对N和U散射的影响)

       表1给出了在只考虑三声子散射的情况下，不同谐波IFCs和非谐波IFCs得到的κ。将无应力的谐波IFCs和小应变下的非谐波IFCs组合得到的值为4032.3 W m-1 K-1。将小应变下的谐波IFCs和无应力的非谐波IFCs组合得到的值为3507.0 W m-1 K-1。通过对无应力κpure= 3524.9 W m-1 K-1的比较，可以看出在小应变下，非谐波IFCs对κ的贡献比谐波IFCs大得多。因此，小应变下声子寿命的增加主要是由于声子软化导致的非谐IFCs减少造成的。而大应变则不存在这种关系，谐波IFCs和非谐波IFCs对κ的影响在数值上大体相似。因此，大应变的高散射率的主要原因可能是金刚石中声子散射通道的增加，这是色散关系的改变造成的。散射相空间的增强会增加声子散射率。

       从图4可以看出，小应变下声子的加权相空间变化最小，而大应变下声子的加权相空间明显变大。这支持了之前的猜想，即小应变下声子寿命的增加主要是声子软化造成的，而大应变下声子寿命的减少主要是与色散变化相关的声子散射通道的增加造成的。

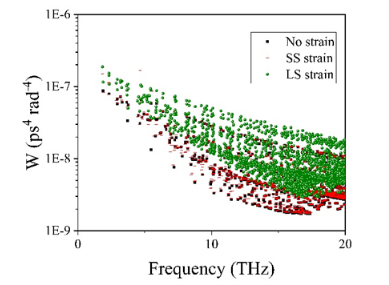
图4 应变金刚石的加权相空间分布

       总结与展望

       该研究通过第一性原理+声子玻尔兹曼方程预测了体金刚石在不同尺度拉伸应变下的热导率变化情况，研究发现了小尺度拉伸应变下金刚石热导率的异常增加和大尺度拉伸应变下热导率大幅降低的现象，并探究了其内在机制。这些发现将指导分析其他类金刚石结构中热导率对应变的依赖性，如IV族元素基材料。小尺度拉伸应变下金刚石展现的超高热导率表明，可以利用局部应变通过建立人工导热通道来调节材料的热导率。

       参考文献

[1] Y. Li, X. Liu, G. Yang, K. Liu, J. Zhao, S. Zhang, L. Yang, B. Dai, J. Zhu, J. Han, Thinning strategy of substrates for diamond growth with reduced PCD rim: design and experiments, Diamond and Related Materials 101, 107574 (2020).

[2] H. Sumiya, K. Tamasaku, Large defect-free synthetic type IIa diamond crystals synthesized via high pressure and high temperature, Japanese Journal of Applied Physics 51, 090102 (2012).https://iopscience.iop.org/article/10.1143/JJAP.51.090102/meta.

[3] A.V. Inyushkin, A.N. Taldenkov, V.G. Ralchenko, A.P. Bolshakov, A.V. Koliadin, A.N. Katrusha, Thermal conductivity of high purity synthetic single crystal diamonds, Physical Review B 97, 144305 (2018).https://doi.org/10.1103/PhysRevB.97.144305

[4] C. Dang, J.P. Chou, B. Dai, C.T. Chou, Y. Yang, R. Fan, W. Lin, F. Meng, A. Hu, J. Zhu, J. Han, A.M. Minor, J. Li, Y. Lu, Achieving large uniform tensile elasticity in microfabricated diamond, Science 371, 76 (2021).https://doi.org/10.1126/science.abc4174

[5] C. Liu, X. Song, Q. Li, Y. Ma, C. Chen, Superconductivity in compression-shear deformed diamond, Physical Review Letters 124, 147001 (2020).https://doi.org/10.1103/PhysRevLett.124.147001

[6]D.A. Broido, L. Lindsay, A. Ward, Thermal conductivity of diamond under extreme pressure: a first-principles study, Physical Review B 86, 115203 (2012).https://doi.org/10.1103/PhysRevB.86.115203.