超硬材料网

       本期论文成果介绍基于第一性原理的金刚石薄膜热导率神经网络预测研究，为团队博士生王彪在《中国科学：物理学 力学 天文学》发表的关于金刚石薄膜热导率预测的最新研究。

论文信息：王彪, 任海杰, 曹文鑫, 胡彦伟, 何玉荣, 韩杰才, 朱嘉琦

https://doi.org/10.1360/SSPMA-2022-0036

通讯作者：朱嘉琦教授

01研究背景

       近年来, 随着大功率、高发热组件小型化、集成化的发展, 电子元器件的散热问题得到了广泛的关注, 如电子芯片、雷达系统和先进的射频系统等。高性能意味着大的散热需求, 尖端技术的发展与冷却系统的冷却能力密切相关。金刚石具有超高的导热系数、无与伦比的机械强度、优异的热力学特性等一系列卓越性能, 是实现“后摩尔”时代电子、光电子、量子芯片以及芯片散热的基础性材料之一。然而随着电路中的电子元器件尺寸达到微纳量级, 尺寸效应将极大影响金刚石的散热特性, 因此, 对金刚石热导率进行跨尺度分析有利于微纳电子元器件的设计和热管理。而玻尔兹曼输运方程是描述多尺度声子输运现象的理想工具，然而因其高维性，利用其对不同尺度金刚石的热导率进行数值求解预测极具挑战性。

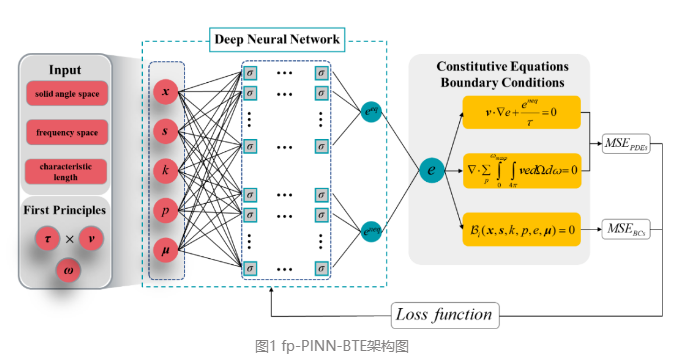
       作为一个专门用于求解非线性偏微分方程的深度学习框架, 物理信息神经网络(Physics-Informed Neural Network, 简记为PINN)的提出[1]为BTE的求解带来了新的曙光, 与传统的基于网格的方法（例如有限元方法）相比, PINN通过利用DNN的自动微分避免了偏微分方程(Partial Differential Equation, 简记为PDE)的离散化, 其对于PDE的求解能力可以有效的解决BTE的强非线性问题。相较于纯数据驱动的神经网络, PINN中施加了物理信息约束, 因此能用更少的数据样本学习得到更具泛化能力的模型[2]。Li等人[1]将基于能量的声子-玻尔兹曼方程[3]嵌入到PINN中, 并命名为PINN-BTE, 以硅的声子色散关系和文献[4]中硅声子弛豫时间表达式作为输入, 通过最小化控制方程和边界条件的残差来预测声子能量分布, 新的神经网络对于单晶硅的预测效果良好。然而, 目前此方法对于金刚石这种高热导率材料的预测能力尚未可知, 对输入样本数据的计算方法也需进一步扩展。本文基于第一性原理，结合以玻尔兹曼输运方程为物理信息的神经网络，有效地预测了金刚石内声子的多尺度热输运问题，并与线性化玻尔兹曼输运方程的求解结果对比，两者具有较高一致性。

02 研究内容

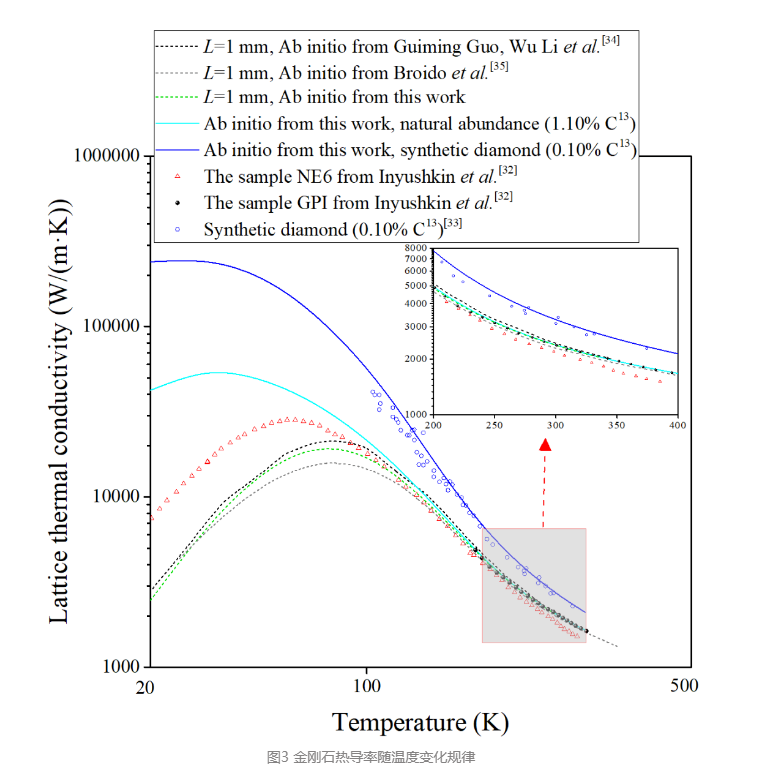
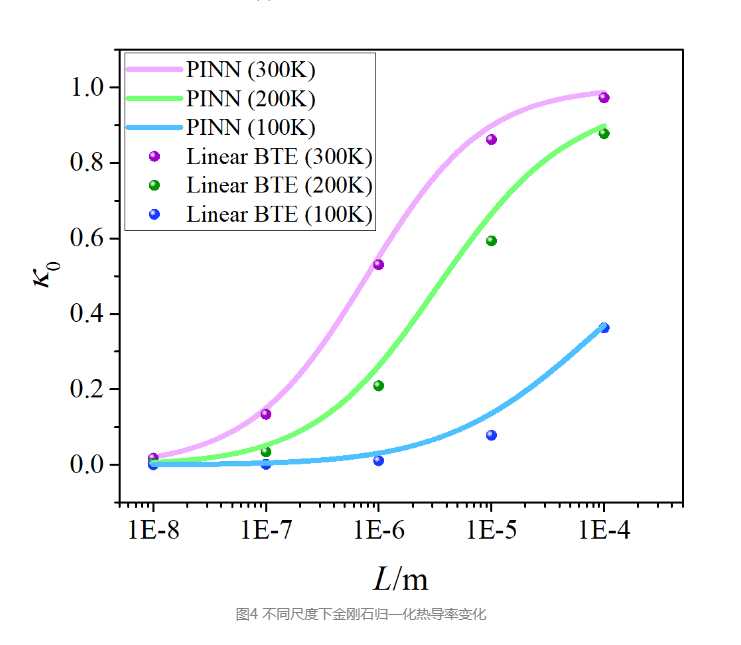
       图4为神经网络预测结果, 展示了不同金刚石薄膜厚度下的归一化热导率随特征尺寸L的变化规律。

       通过和线性化BTE迭代求解的结果进行对比, 两者展现了相同的分布规律和变化趋势, 从图中可以观察到, 金刚石由于其较长的声子自由程, 其热导率在毫米尺度便已经出现了尺寸效应, 同一温度下, 尺度越小, 金刚石归一化热导率越低, 而温度越低, 尺寸效应在热导率上表现得越明显, 即相同尺度下归一化热导率越低, 这和之前阐述的规律是一致的。

       由于fp-PINN-BTE中用的是基于能量单模弛豫时间近似的BTE模型, 输入的声子散射率为零阶声子散射率, 因此训练过程中会对体热导率有所低估, 最终导致由fp-PINN-BTE训练得到金刚石归一化热导率相对于线性化BTE迭代求解结果有些许偏差。然而, fp-PINN-BTE在计算资源和效率上相比于线性化BTE迭代求解的巨大优势是不容忽略的。

       图5 展示了特定温度域和特征尺寸域下拟合的归一化热导率曲面, 立足于已有预测点, 通过使用Delaunay 三角剖分执行插值将归一化热导率的范围扩展到整个温度域和特征尺寸域。鉴于数据点数量和拟合方法等因素, 此曲面可能与实际情况存在些许差距。未来将用物理信息神经网络在物理规律上做出更多的改进, 扩充多温度下不同尺度归一化热导率的结果, 并建立相应数据库。

03 总结和展望

       本文研究了金刚石热导率在不同尺度范围内的变化规律。首次将基于第一性原理计算获得的金刚石声子信息作为PINN-BTE的输入样本进行训练, 得到了不同金刚石薄膜厚度下的归一化热导率, 通过和线性化BTE迭代求解的结果进行对比, 两者展现了相同的分布规律和变化趋势; 验证了PINN-BTE方法在超高热导率材料上的适用性, 热导率尺寸效应预测结果的规律和趋势是相对准确的, 然而对金刚石的预测精度却不如硅, 可见PINN-BTE方法在个别材料热导率的预测上依然存在一些限制。且由于PINN-BTE中采用的是基于能量单模弛豫时间近似的BTE模型, 输入的声子散射率为零阶声子散射率, 这无疑会在声子正散射占主导的金刚石材料的计算上产生误差, 预测过程中会对绝对热导率有所低估, 归一化热导率有所高估; 金刚石由于其较长的声子自由程, 其热导率在毫米尺度便已经出现了尺寸效应, 同一温度下, 尺度越小, 金刚石归一化热导率越低, 而温度越低, 尺寸效应在热导率上表现得越明显, 即相同尺度下归一化热导率越低。随尺度的变化, 金刚石每个模态的声子热导率具有相似的变化规律。PINN-BTE在绝对热导率预测和超高导热材料归一化热导率预测中的不足有待进行更深的研究, 且当金刚石薄膜的厚度仅为数个原子时, 所展现出的新声子模式有待进一步发掘。

参考文献：

       [1] Li R, Lee E, Luo T. Physics-informed neural networks for solving multiscale mode-resolved phonon Boltzmann transport equation. Mater Today Phys, 2021, 19: 100429

       [2] Li Y, Chen S C. Physics-informed Neural Networks: Recent Advances and Prospects. Comput. Sci. (in Chinese). 2021 [李野, 陈松灿. 基于物理信息的神经网络：最新进展与展望. 计算机科学, 2021]

       [3] Zhang C, Chen S, Guo Z, et al. A fast synthetic iterative scheme for the stationary phonon Boltzmann transport equation. Int J Heat Mass Transfer, 2021, 174: 121308

       [4] Terris D, Joulain K, Lemonnier D, et al. Modeling semiconductor nanostructures thermal properties: The dispersion role. J Appl Phys, 2009, 105(7): 073516