人造金刚石合成工艺基础
王光祖

编者按：
        本文系王光祖先生在自藏文稿丛中发现的一份技术文稿。1963年6月正值我国第一颗人造金刚石研制的攻坚阶段。这是作者以《人造金刚石合成工艺基础》主编的身份，向研制小组部分成员做的一次学术报告。时隔45年，文稿虽已泛黄，但更显其历史性的珍贵。它在总结早期研究者们的经验教训基础上，指出了我们研制工作应遵循的原则和主攻方向；它不仅从热力学、动力学角度对人造金刚石合成机理做了具体阐述，而且对试验研究工艺，诸如，主要原材料的选择、试块的组装形式、压力温度条件等做了详尽说明。历史的实践证明，它不愧是我国第一颗人造金刚石诞生的催产素。
        经征得作者本人同意，本刊特将此文稿呈现在读者面前，使我国现在从事金刚石研究的科技工作者们了解和学习我国第一颗金刚石的科学工作者们的科学态度、严谨作风，愿其对人造金刚石向深层次探密，能起到启示和鼓舞作用。

地    点：通用机械研究所
时    间：1963年6月26日
报告人：王光祖
参加者：于鸿昌 芦飞雄 胡恩良 金秋野 许锦枫 余征民 孙荣传 周纪堂 姚裕成 柳开忠 熊文松 张永华

摘要：
        根据《人造金刚石合成工艺基础》编写提纲的要求，我们着重对石墨—金刚石转变过程中热力学条件的分析及其平衡曲线的讨论、石墨—金刚石转变过程中动力学条件的分析、石墨—金刚石转化过程的催化、试样加热方法的讨论和加温加压过程的分析。在分析上述问题的过程中，曾向北京大学化学系孙承谔教授和华东纺织工学院化学系染化教研组陈美华老师请教过有关理论问题。提出了关于《人造金刚石合成工艺基础》编写原则的几点考虑：1、为人造金刚石晶体生长第一阶段实验提供理论上的依据；2、通过对石墨—金刚石转变过程的热力学和动力学条件，以及触媒在这一转变过程中的作用的初步分析，来了解金刚石晶体生长的一般规律；3、有关金刚石晶体生长的细节问题，如活化能、反应速率的计算等问题在编写人造金刚石工艺基础(第一阶段)一文时暂不加考虑，但必须指出，这一理论工作是一定要做的。

        一、序言
        人造金刚石晶体生长技术是最近几年才发展起来的一门新技术，它与晶体生长、结晶学、高压、固体物理学、化学热力学和化学动力学是紧密联系着的，尤其是晶体生长和高压物理学最为密切。
        近代，随着高压物理学的深入研究和超高压技术的迅速发展，人造金刚石晶体生长技术也就很快地为人们所掌握了。这一研究之所以为世界科学工作者给予如此重视，其原因不仅是因为金刚石硬度在工业上具有突出作用，更重要的是它具有技术的先进性和经济的合理性(与天然金刚石比较)，以及天然金刚石是一种极其稀有的非金属矿物，根本不能长期满足科学技术飞跃发展的需要要求等客观原因所致。
        近百年来，人们力图能够获得合成金刚石这一强烈愿望，给超高压高温技术的研究起着极大的推动作用，如所周知，超高压高温技术的进一步提高，不仅对金刚石合成技术和理论的研究具有实际意义，同时也为促使其它学科(如实验地质学)的深入研究和探索新物质开辟了广阔途径。
        从所发表的有关资料来看，人造金刚石合成技术的研究中心已在好些国家建立起来，正在大力展开这方面的研究工作，并取得显著成效。这一技术轮廓虽有透露，但关键性的细节问题仍属保密，有待我国科学工作者去研究解决。因此，我们认为:

1. 天然金刚石不能满足科学技术发展的要求，必须走人工合成之路；
2. 从国内天然资源少，需求量多，必须迅速地掌握人造金刚石晶体生长这一门新技术；
3. 为了给人造金刚石新品种的发展提供一套完整的工艺规程，必须在实验室中进行创造性的实验研究工作；
4. 为了给实验研究工作提供一些方向性的资料，特将收集到的国外有关人造金刚石合成技术资料，工艺资料加以整理分析，编写了“人造金刚石合成工艺基础”。供实验研究参考。

        二、人造金刚石研究简史

        1880年英国化学家Hannery，1894年法国著名物理学家Moissan和1935～1940年美国杰出高压物理研究者P.W.Bridgman等几个著名的和具有代表性的实验，对20世纪50年代人们掌握人造金刚石合成技术做出了贡献。清楚地证明，人造金刚石的合成过程必须是一个超高压、高温同时并举的过程，也就是说，祗有在超高压高温同时存在的条件下金刚石生成才有可能。关于这点，当然从天然金刚石的形成也会使我们这样想。P.W.Bridgman的试验告诉我们，在人造金刚石晶体生长的研究中，除首先必须考虑这一转变的可能性，但更重要的是研究使可能性变为现实性的具体条件，也就是我们常说的反应速率问题。

        三、石墨—金刚石转变过程中热力学条件分析及其平衡曲线的讨论

        热力学原理及其数据是计算与讨论石墨—金刚石平衡曲线的基础，也就是说，在研究石墨—金刚石的转变过程中，首先应考虑到的是热力学问题，因为热力学的计算使我们能够预测石墨—金刚石转变过程的方向问题，从而为研究这一转变过程提供理论上的依据。
        (一)热力学基础
        前面讲过，根据热力学原理可以确定石墨—金刚石转变过程的方向和限度，其转变过程的方向可以通过转变过程的自由能的变化来判断。
在一定温度下反应自由能随压力的变化率可以下式表示。

(1)

积分(1)式得:

(2)

在等温条件下:
由此式(2)可改写为

(3)

        式中: ，，分别表示在压力为零和温度为T时自由能，热焓、熵的变化；表示压力为P和温度为T时自由能的变化；为石墨-金刚石转变反应中二者体积差。
        式(3)的物理意义是表示在一定温度下，反应自由能随压力的改变关系式。
        若(1)>0，石墨的热力学稳定区，不生长金刚石。
        (2) <0，金刚石的热力学稳定区，可得到金刚石。
        (3) =0，金刚石和石墨处于平衡状态。
        (二)平衡曲线的计算
        关于平衡曲线的计算早在1912年Pilitzer就用不十分精确的燃烧热值对金刚石生长条件做过计算。
        后来，1920年Mitheng，1926年F.Simon，1938年F.D.Rossini，R.S.Jessup和О.И.Лейпунский，1945年D.D.Wagman，Taylar等，以及1955年Berman和Simon根据热力学原理对石墨—金刚石平衡曲线都做过计算。由于各个研究者所采用的数据不一样，因此所得到的数据不完全吻合。在分析平衡曲线的工作中，我们根据各个研究者所采用的热力学数据进行过演算。总的来说，祗要有以下热力学数据就可计算，例如，石墨和金刚石的热容、热焓、熵、克分子体积等。但必须说明的一点就是目前测定的这些数据的最高温度仅能达到1200K。Berman和Simon的石墨—金刚石平衡曲线在1200K以下部分就是通过以上所提到的热力学数据计算得到的，高于1200K以上部分采用了直线外推。

О.И.Лейпунский在推算高于1200K石墨—金刚石平衡曲线采用了下式，即，
ΔZ=ΔZ―(T―T0)ΔS0―ΔZ0[lnT/T0―(T―T0)]
并假定T0=1400K
ΔZ1400=1880
ΔS1400=-1.16
ΔCp=-0.1(根据Kелль方程式计算，ΔCp=+0.1)。
我们对瑞典Lilijeblad曲线在61000atm和3000K时为什么发生大幅度的弯曲做了分析和演算。
Lilijeblad所采用的数据为:
αDia=3.6×10-5度-1 βDia=1.5×10-7atm-1
αGr=2.7×10-5度-1 βGr=3.6×10-6atm-1

        根据以上数据计算得到的结果如表1所列。

表1压力与温度的关系

T/K	P/atm	T/K	P/atm
1500 1700 1900 2100 2300 2400 2500	43212 47923 51197 53770 55327 55604 55511	2600 2700 2800 2900 3000	55502 54662 53648 52305 50638

        如果用A.R.Thewlis1956年在1200K所精确测定的数据，即α=0.8×10-5度-1来推算(并指出在高温时无反常膨胀)，则将得出完全不同的结果，如表2所列数据

表2 压力与温度的关系

T/K	P/atm	T/K	P/atm
1500 1700 1900 2100	43377 48417 53448 58475	2300 250 2700 2900	63496 66510 76189 81009

        以上平衡曲线均系理论曲线，除以上理论曲线外，还应特别指出的曲线就是美国通用电气公司(G E Co)的石墨—金刚石的实验曲线，如图1所示。

图1 G E Co实验曲线 图1 G E Co实验曲线

        1500～2700K曲线部分是G.E.Co研究者的实验曲线。高于2700K的曲线是外推值。这条曲线对于人造金刚石晶体生长的研究具有更大的实际意义。
        (三)平衡曲线的讨论
        1、在低于1200K曲线部分大体上是一致的，低温时(0～40K)曲线向上弯曲是因为金刚石昀反膨胀之故。
        2、如Bermon和Simon曲线，在1200K以上时，假定dP/dT=27而进行外推的，而О.И.Лейпунский在1400K以上则假定dP/dT保持25来外推的。但实际上，曲线斜率(dP/dT)是随温度上升而逐渐减小的，即在1200K，2200K，3000K时dP/dT分别为27，25，23(应考虑金刚石的反常膨胀现象)。
        3、由此可知，Berman，Simon，Лейпунский在高温条件下，由外推法所得之平衡压力实际上是偏高，越往高温这种差别也就越大。
        4、根据上述情况，我们建议按dP/dT分别为27，25，23的修正曲线做为我们的实验曲线。
        为计算方便可采用下式来推算某一高温下的平衡压力。

P(atm)=B+mT/K
P-平衡压力; B-截距
m-斜率; T-绝对温度/K
当T>1400K时 B=6500m=27
当T>2200/K时B=10 000 m=5

        (四)石墨金刚石转变过程中动力学条件的分析
        石墨—金刚石的热力学研究表明，祗要温度和压力处于“金刚石的热力学稳定区”内，石墨就有转变为金刚石的可能，但实际情况并不如此理想。例如，1935～1940年间P.W.Bridgman在室温和400 000atm和600℃，75 000atm，以及1956年H.T.Hall在约3000℃，100 000atm的超高压高温条件下都没有能由石墨直接制得金刚石，这些有力的例证告诉我们，动力学问题是极其重要的问题。
        可是，在动力学条件的分析过程中，由于缺乏必要的数据及需要复杂的量子力学计算，其中最主要的原因应该是缺乏必要的数据，其次某些数据虽收集到，但非公认的。根据这些数据我们做过一些计算，从计算所得到的结果来看还有问题，因此只能就有关问题做点定性说明，定量说明恐怕要在我们实验取得某些成效之后才有可能。
        现在我们就根据log速度=常数―(PΔV*/RT)来讨论石墨→金刚石反应速度问题。在未讨论这一问题之前，对上式的由来做一简要的推导。
根据近代碰撞理论可知，不是所有分子都能参加反应的，参加反应的只有活化分子碰撞形成活化络合物(即处于过渡状态)，这个络合物是不稳定的，它分解后可得到“生成物”对石墨—金刚石的转变过程来讲，可以下式表示。

CGr→C*Gr→CDia
C*Gr-过渡状态的活化分子
假定C*Gr分解时浓度为C*
则反应速度=C*/t，t为分解时间，
因为，t=1/ν
所以，反应速度=C*ν，C*=?
按统计规律近似等于KT/hν
式中: K-波兹曼常数 1.38×10-16尔格/度
h-普朗克常数 6.55×10-27尔格/秘
ν-振动频率
C*’=C*(KT/hν)，C*络合物总浓度。
由此可求出反应速度=C*(KT/hν)×ν=KT/hC*
C*=?
为讨论方便起见，假定活化络合物和反应物之间有一平衡状态。
则K*=C*/CGr，K*活化络合物平衡常数
C*=K*CGr
代入上式即得反应速度=(KT/h)K*CGr，
如果把它和通常的反应速度表示法比较
反应速度=KrC
则反应比速Kr为:
K*=(KT/h)K*
根据热力学定律得知，若令ΔZ*表示标准状态时，活化过程自由能的变化，则它与平衡常数K*问的关系为:
ΔZ*=―RTlnK*
K*=e―ΔZ*/RT
代入上式即得，Kr=KT/he―ΔZ*/RT或KT/he―PΔV/RT
ΔV*表示活化络合物与石墨克分子体积差，即
ΔV*=V*活化络合物―VGr
最后将上式一变则为:
Log速度=常数―PΔV/RT

        当其它条件不变时，增加压力对于反应速度是不利的，这是因为压力的增加对于庞大和开阔活化络合物的形成是不利的。
        （五）石墨—金刚石转变过程的催化
        压力和温度是影响反应速度的重要因素。石墨转变为金刚石只有在两种条件同时存在时才能实现。据推测，在无触媒参与的条件下，这一转变过程的反应压力和温度必须不低于190 000kg/cm2和∽3900℃，这一推测的正确性已为实验所证实。不过目前要得到这样高的压力和温度的设备是非常困难的。
        为了解决这一难题，国外的研究者在人造金刚石晶体生长技术方而进行了不少工作。他们的研究结果充分表明，在较低的温度(1200～2400℃)和压力(50 000～100 000atm)的条件下，几分钟内是能够制得金刚石的，不过需要加入触媒剂。十分明显，触媒在这一转变过程中是非常重要的。在目前我们所设计的61型、62型超高压高温设备所能达到的压力(75 000atm)和温度(1200～2000℃)的范围则更具有其现实意义。不言而喻，触媒的正确选择也就显得十分重要。
        （六）关于选择触媒问题的考虑。
        （1）触媒的重要作用在于它能降低活化能的能量，从而使活化分子的相对数目增大，这样对于增大某一过程的反应速度极其有利的观点出发，在目前我们设备所能达到的条件下，触媒的应用应视为由石墨转变为金刚石过程中的重要条件。
        （2）一般来说，触媒熔点是随压力的提高而有所提高的(每增加1000kg/cm2，其熔点约提高0.2～2℃)，可是触媒只有在熔融的状态下才能起到其应有的作用。另从石墨—金刚石平衡曲线关系看来，温度越高所要求的平衡压力越高，由此可知，选用低熔点约金属或合金作添剂是较合适的(选用碳和金属或合金共晶点低的触媒更为恰切些)。

图2 不同金属触媒的压力-温度平衡曲线

        以上金属的熔点的顺序为: Rh1966℃，Pt1774℃，Pd1555℃，Fe1539℃，Ni1455℃。
        但实际合成压力温度高低的顺序是:Fe，Ni，Rh，Pd，Pt
        （3）通过活化能的计算，确能从理论上预测那些触媒对于石墨转变为金刚石是有利的。但在目前计算数据不完整和缺乏的情况下，在较短时间内要想通过这一途径来解决触媒的选用问题是有困难的。为此我们确定，在试验研究的最初阶段，可从国外常用的、成熟的触媒，而且所要求反应压力，温度较低的触媒中挑选出几个来进行试验，这些触媒是Ni、Fe、Ni80-Cr20、Ni30-Fe66-Cr4和Ni—Ge(30～35Ni，70～65Ge)。
        根据所选定的触媒，将人造金刚石的生成条件区分成第一、第二两个合成实验区。合成实验步骤分成第一，第二两个阶段。第一阶段按第一区域进行合成实验，因为第一区域具备下列优越条件:
        我们设的61型，62型设备性能所能满足的区域。
        在中温中压地带较易施行。
        目前人造金刚石合成一般所采用区域。

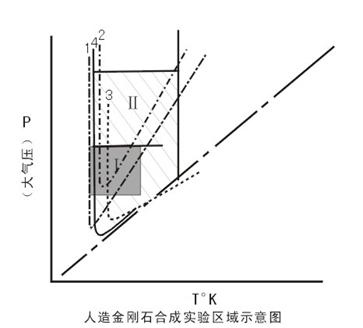
图3 人造金刚石合成实验区域图

        注:1、Fe66-Ni30-Cr4；2、Ni80-Cr20；3、Ni；4、Fe
        在这一阶段估计能获得第一颗人造金刚石。在第一阶段合成实验成功之后，即转入第二阶段，在第二区域中进行合成实验，主要在于摸清在较低的温度和压力条件下和较高的温度与压力条件下金刚石的生成规律。
        （七）试样加入方法的讨论
        人造金刚石的合成过程是石墨—金刚石的结晶变态过程。因此，石墨是人造金刚石的主要原料。据资料记载，美国G.E.Co根据实验结果认为，使用纯石墨作为原料最好。
        除石墨外还需要加入一定量的触媒，为尽量减少实验中的影响，我们认为，在金刚石晶体生长研究的最初阶段，无论是石墨，还是触媒的纯度都应≥99.9%。
        试样的加入方法:
        a、触媒和石墨混合加入法;
        b、在镍管中填充石墨粉;
        c、石墨和触媒片多层加入法;
        d、在石墨柱体中插入金属丝或棒等。

图4几种不同的组装形式

        如从既要有较大的接触面，又要有过饱和的特性考虑，不难看出，采用(c)的组装形式是有利的。
        （八）试样加热方法的讨论
        目前已知的加热方法大致有如下几种:
        （1）利用反应物直接加热。这种方法的优点是:
        简化工艺;
        能加至很高的温度;
        可直接从功率及电阻的变化来预测金刚石的形成。
        （2）绕丝或碳管加热。
        （3）高频加热，此方法还未发现被人采用。
        （4）利用化学方法。短时能造成高温，但其温度较难控制。
        从方法(1)与(2)对比不难看出，如从工艺过程的简易及考虑今后合成工艺将向更高的温度和压力发展出发，无疑第一种方法是有利的。
        （九）加压加温过程分析
        加压加温过程是人造金刚石合成工艺中的主要操作程序。由石墨-金刚石的热力学条件分析得知，石墨转变为金刚石的压力和温度必须是处于“金刚石的热力学稳定区”内，怎样才能使压力和温度达到“金刚石的热力学稳定区”?概括地说可通过以下方式来实现:

1. 先升压，后升温;
2. 先升温，后升压;
3. 沿石墨-金刚石平衡线同时升压升温;
4. 交替式升温升压。

        在现有设备条件及技术水平下，为保证设备使用寿命、绝热材料的性能及便于控制考虑，采用第一种方法。待完成第一阶段任务后及设备条件有了进一步的改善和对设备性能有了进一步掌握之后，还有必逐步对后三种方法进行探索。
        降压降温步骤:为使已形成的金刚石趋于稳定，必须先降温，待温度降至100℃或更低时才降压。
        以上是笔者所做的关于“人造金刚石合成工艺基础”的主要内容。因限于技术水平，资料的不足，以致制订出来的合成工艺方案，多系设想，不够完善，因而有必要在实验研究工作进行过程中不断经实际检验，及时纠正与充实。最后，敬请各位审查并希望提出宝贵意见。
        金刚石合成成功后，还有两项重要工作就是理化检验和分选，我们所有专人在进行。