摘要 引言无心磨削工艺由于其生产效率高、自动化简易操作和高精度的特点而广泛应用在圆柱形零件的精加工制造中。对表面粗糙度和圆度误差进行优化则有利于改善无心磨削工艺。例如通过导轮速度、进给速...
作者:Phan Bui Khoi, Do Duc Trungb, Ngo Cuongb
引言
无心磨削工艺由于其生产效率高、自动化简易操作和高精度的特点而广泛应用在圆柱形零件的精加工制造中。对
表面粗糙度和圆度误差进行
优化则有利于改善无心磨削工艺。例如通过导轮速度、进给速度和切割深度参数的最优化来减小工件表面粗糙度和圆度误差;建立经验模型来减小表面粗糙度;推演出运算法则来设置最优化工作条件等。
本实验通过对20X渗碳钢进行磨削加工得出表面粗糙度和圆度误差的最小值,以此作为切入无心磨削工艺的优化研究。输入参数有:纵向修整进给速度(Ssd)、切入进给速度(Sk)、中心高度角(β)和导轮速度(Vdd)。
1. 实验
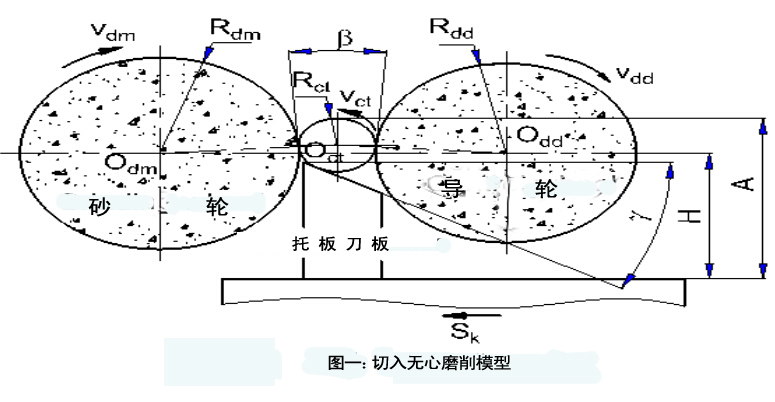
无心磨削模型:
图一是切入无心磨削模型,通过A值大小来调整中心高度角(β)。β和A的关系式如下:
式中的H为
砂轮中心和导轮中心到无心磨床托板刀板的距离。
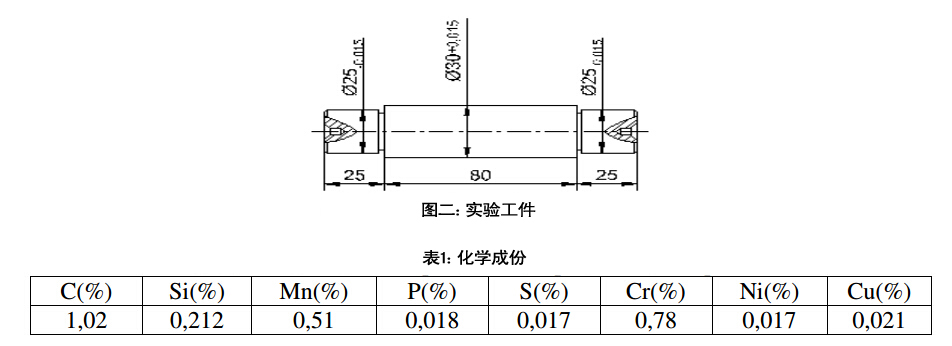
工件:
20X渗碳钢(62HRC);图二中的工件由特制的30°角托板刀板支撑;表1为实验化学成分:
砂轮:刚玉砂轮Cn80.TB1.G.V1.500.150.305x35m/s。
机床:M1080B无心磨床,H=210mm,如图三所示:
测量设备:
千分表测量圆度误差,精准度为5/10000,每个工件测量三次;日本三丰Surftest表面粗糙度测量仪SJ-401,临界值0.8mm。表2中表面粗糙度和圆度误差为连续三次测量所得平均值。
2. 实验矩阵
实验矩阵在无振动条件下操作,保持砂轮速度34m/s,磨削深度0.05mm,修整深度0.01mm,无火花磨削时间1s,冷却液流量恒定。
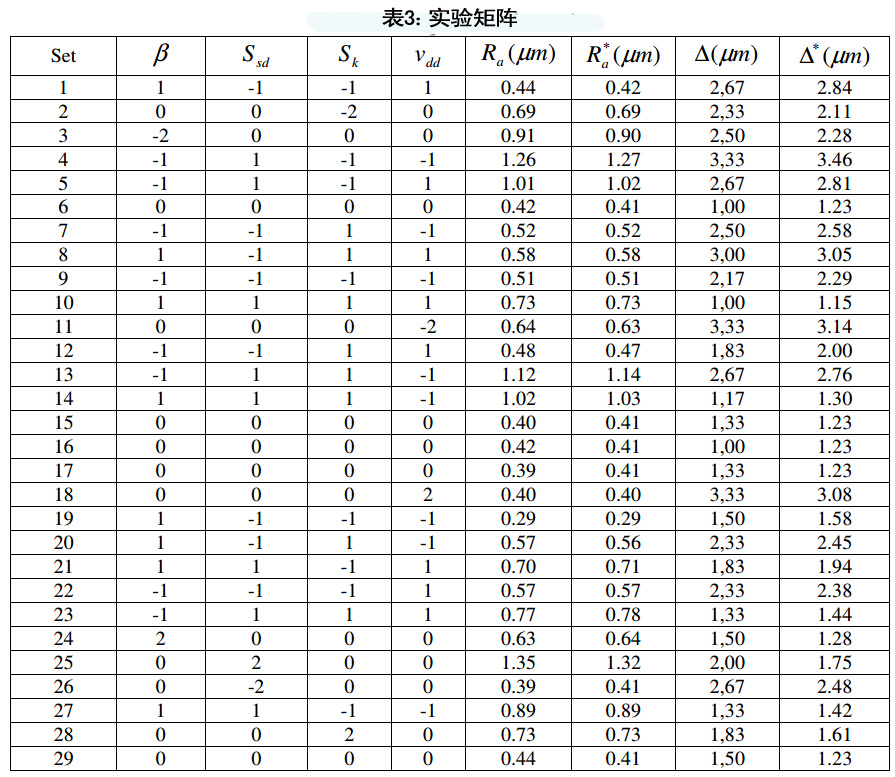
利用中心合成设计,四个输入参数(Ssd,Sk,β,Vdd)值如表2所示。实验矩阵共计29组,其中包括8个轴向点、5个中心点和16个正交点,如表3所示:
输入参数对输出参量的影响
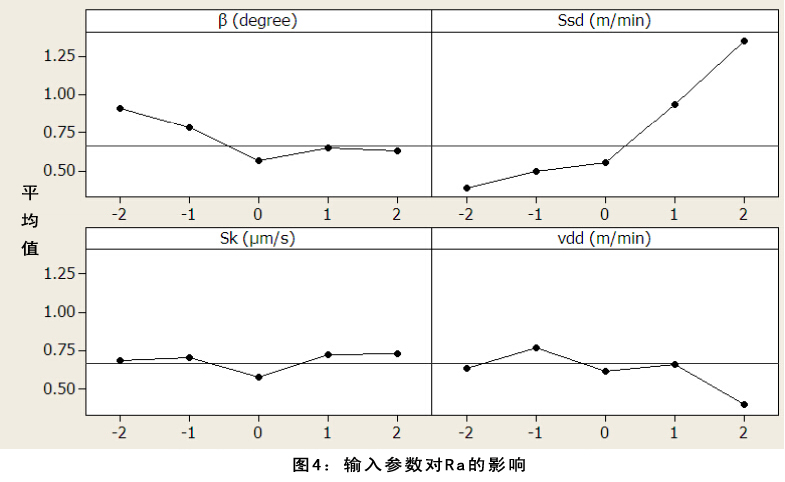
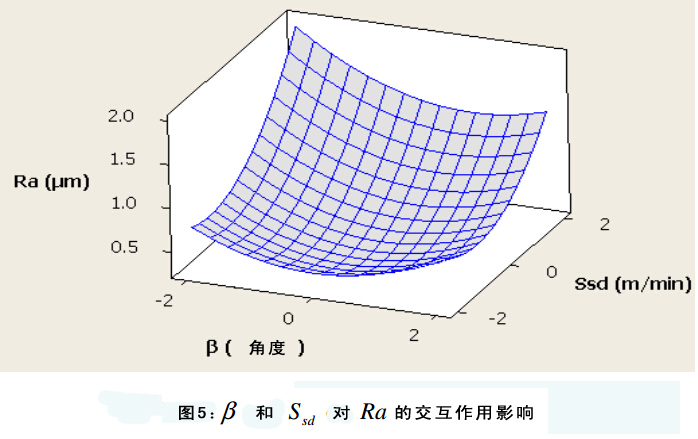
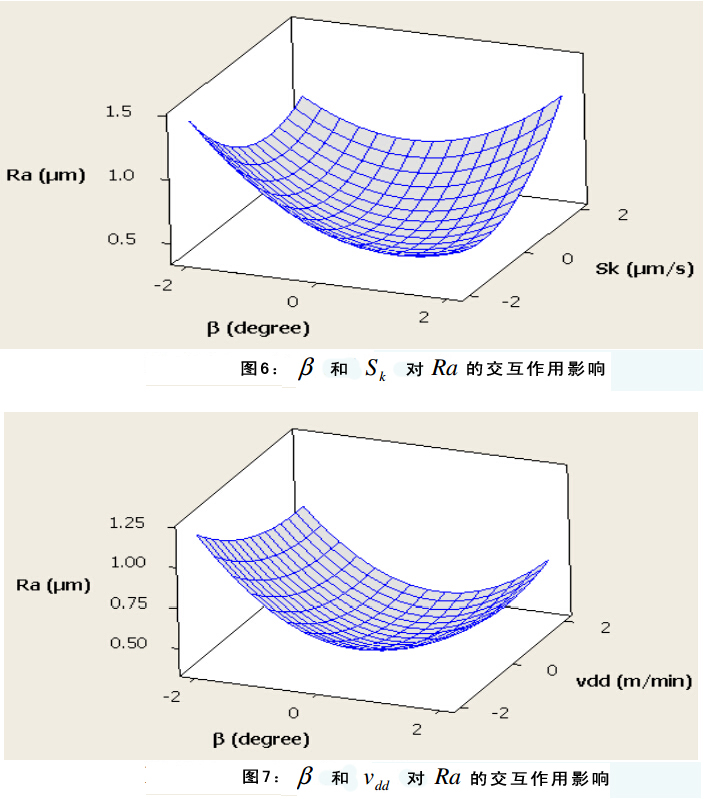
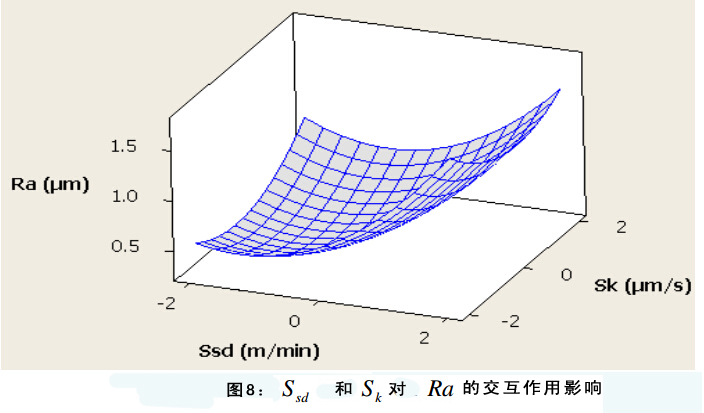
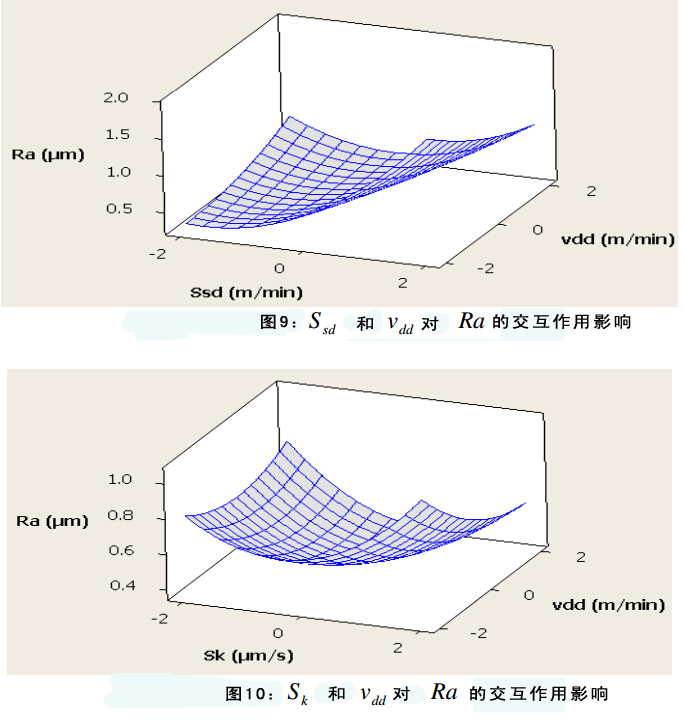
图四展示了输入参数对表面粗糙度(Ra)的影响。图5—10显示了输入参数对表面粗糙度的交互作用影响。在每组图片中有两个变量,另外两个作为恒定中间值。图表显示所有输入参数对表面粗糙度都有显著影响。
输入参数对圆度误差的影响
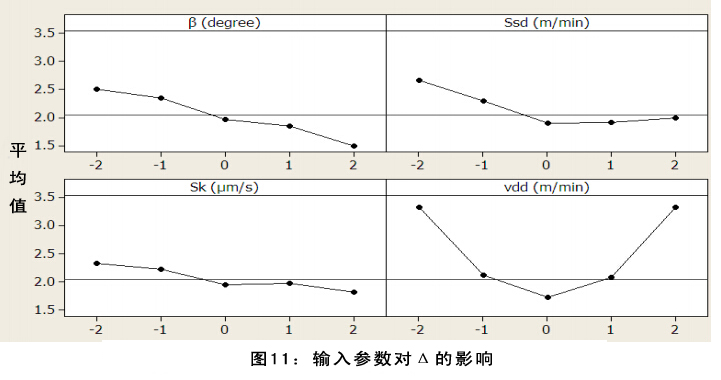
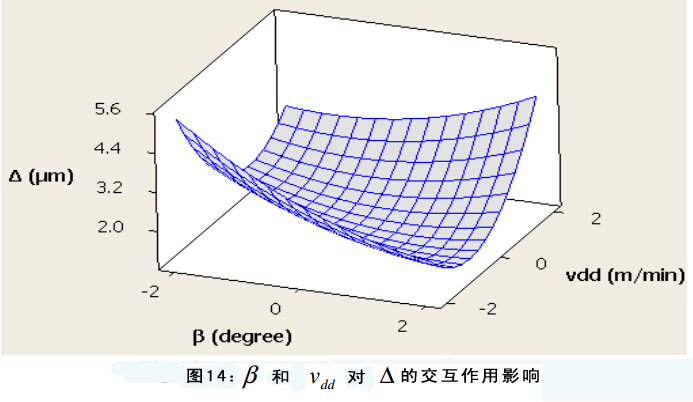
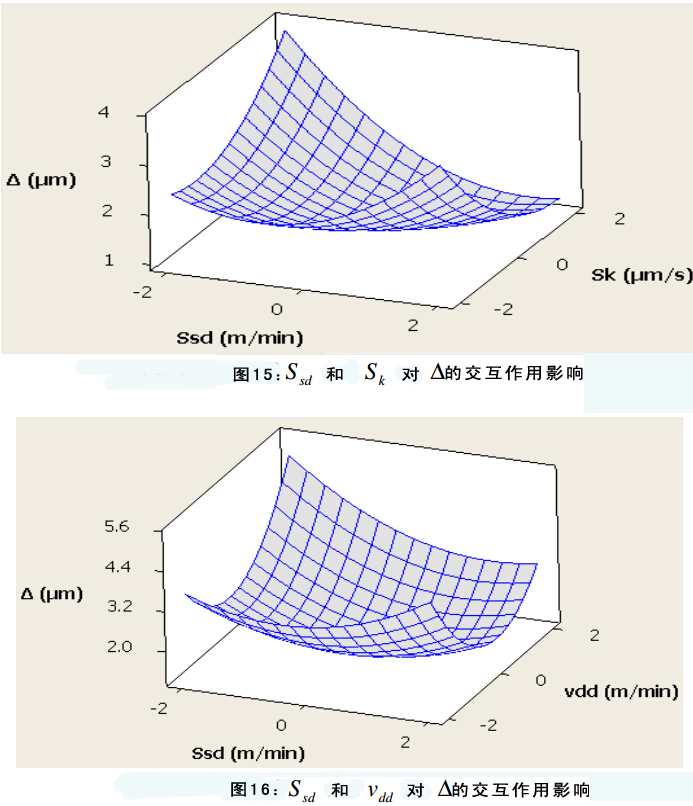
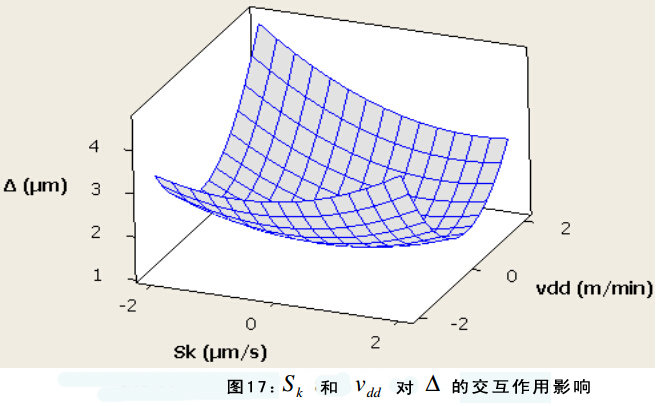
图11展示了输入参数对圆度误差的影响。图12—17显示了输入参数对圆度误差的交互作用影响。在每组图片中有两个变量,另外两个作为恒定中间值。图表显示所有输入参数对圆度误差都有显著影响。
3. 回归模型
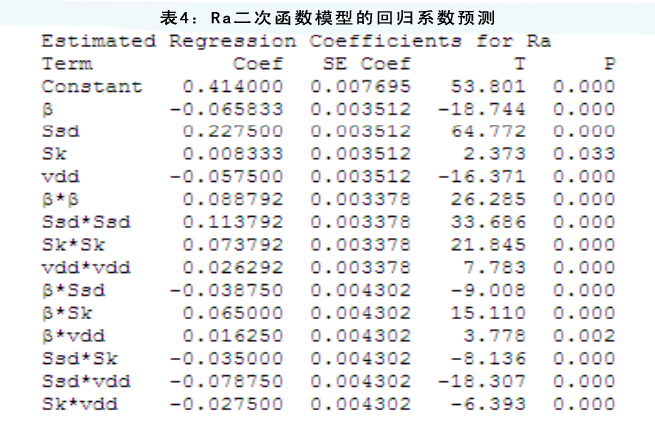
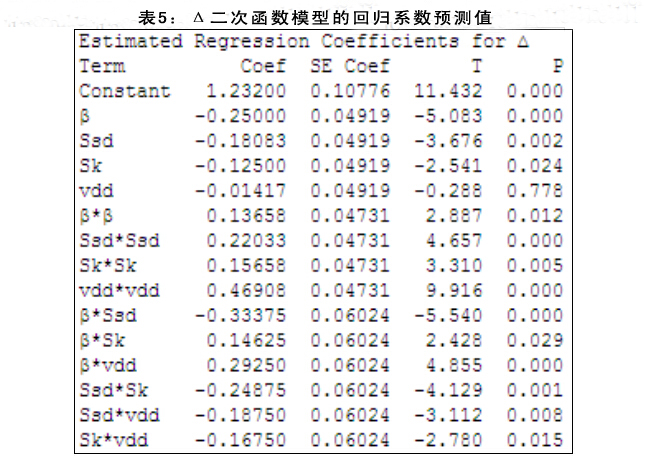
实验利用数据分析软件Minitab 16来设置回归系数。表4和表5分别是Ra和Δ二次函数模型的回归系数估计值。表面粗糙度和圆度误差模型以编码参数的形式用非还原最终方程式表达出来。
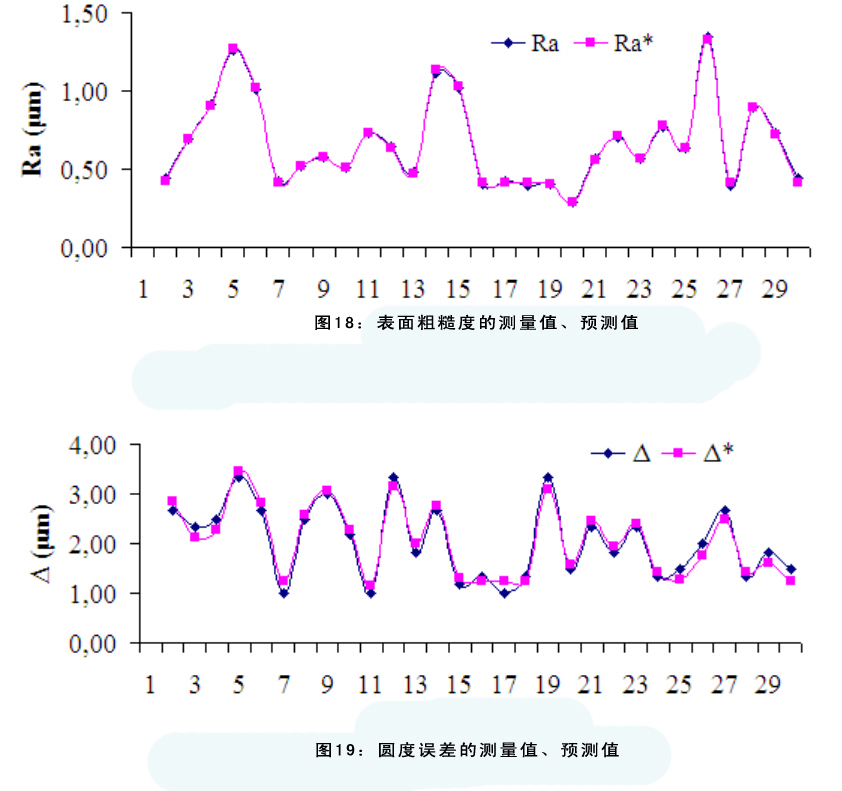
以上模型可以在特殊设计点预测表面粗糙度和圆度误差。表3还给出了预测反应值R*a 和Δ*。图18和19给出了测量值和预测反应值之间的不同。
4. 最优化
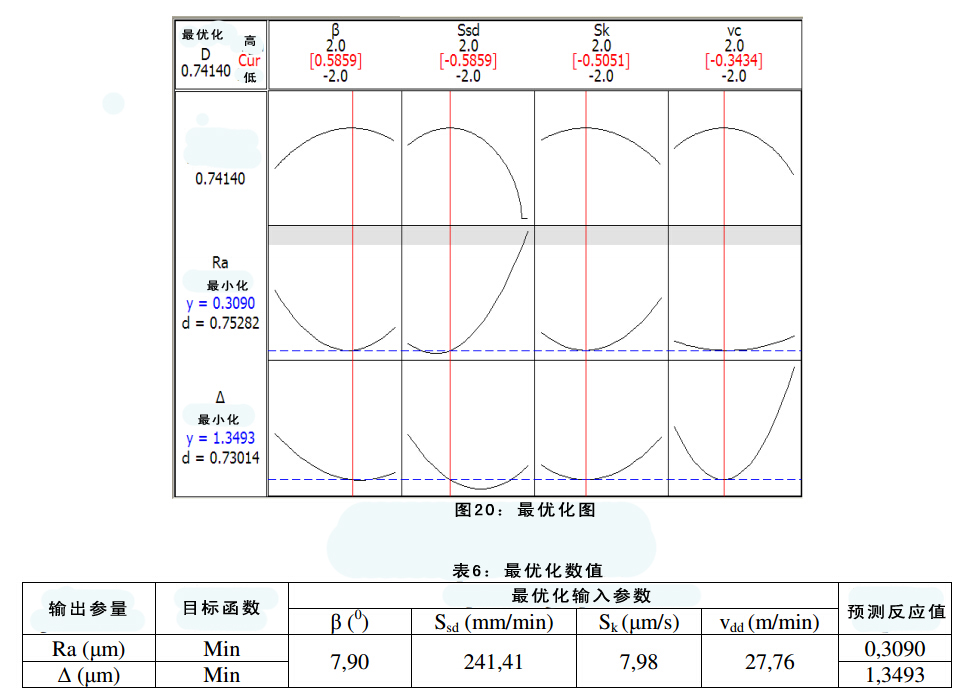
通过最优化处理,将Ra和Δ最小化,而Ra和Δ也会构成多目标最优化问题。试验利用Minitab 16软件来对这些目标进行最优化处理。图20和表6分别是最优化图和数值表。
5. 结论
在对20X渗碳钢加工过程中,所有四个输入参数(Ssd,Sk,β,Vdd)对输出参量、表面粗糙度和圆度误差都有显著影响。因此,为了实现对20X渗碳钢表面粗糙度和圆度误差的最小化目标,Ssd,Sk,β,Vdd的值应分别为241.41mm/min;7.98µm/s;7.9°和 27.76m/min。
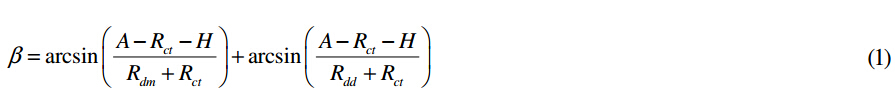







 手机资讯
手机资讯 官方微信
官方微信







 豫公网安备41019702003646号
豫公网安备41019702003646号